Determine o limite infinito. lim x → 0 + ⁡ l n sin ⁡ x

Enunciado

E aí, galerinha! 😊

Nesse problema queremos mostrar que o limite tende ao infinito.

Tem ideia de como fazer isso? 😬

Quando se trata de limite, temos que analisar os valores que as funções tendem a assumir quando a variavel se aproxima de um determinado valor.

Então temos que ter em mente que não estamos buscando o valor exato, estamos buscando o valor que a função tende a assumir.

Veja só! 😉

Analisaremos o limite de:

Como sabemos que quando:

A função seno tende a mas como é positivo seno tambem é positivo, ou seja

Dessa forma, temos que

Quando tende a em , sabemos que o resultado tende a , ou seja

Tranquilo até aqui?

Analisando parte do gráfico da função :

Plotando o gráfico da função com o auxilio de um software, temos

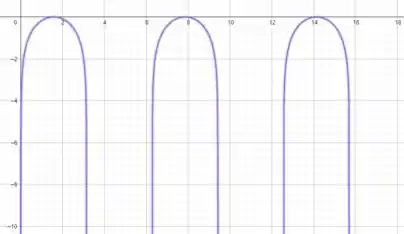
Podemos então, confirmar o que foi encontrado no passo 2:

E aí! o que achou? Responde Aí! 😁