Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 42
Determine o limite infinito.
Passo 1
Fala aí...
Nessa questão devemos analisar o limite lateral:
Um limite lateral é quando queremos ver para onde a função vai quando os valores de tendem a um determinado valor apenas por um lado.
Aqui, queremos ver como se comporta essa função quando tende a zero apenas por valores maiores que zero, ou seja, o limite pela direita dessa função.
Repara que temos duas funções que conhecemos o seu gráfico (se você não conhece, vai conhecer agora e lembrar deles, pois eles são super importantes).
A função que possui o seguinte gráfico:
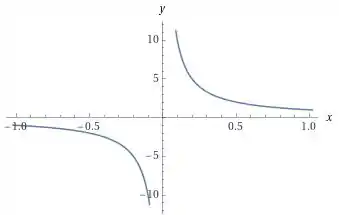
Onde a gente percebe que quando tende a zero pela direita, a função tende a
E a função que possui o seguinte gráfico:
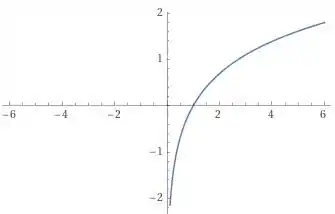
Onde percebemos que quando x tende a pela direita a função tende a :
Passo 2
Analisaremos então o limite de:
Como sabemos que, quando:
Então:
Dessa forma, devido ao sinal negativo que precede , teremos dois números positivos muito grandes sendo somados dentro do limite, sendo assim:
Repare que , ou seja, um número muito grande somado por outro número muito grande, resulta em um número muito grande.
Só precisamos tomar cuidado quando temos , pois isso não resulta em zero e sim em uma indeterminação.
Passo 3
Analisando parte do gráfico da função:
no ponto de interesse, isso é para tendendo a zero pela direita, temos:
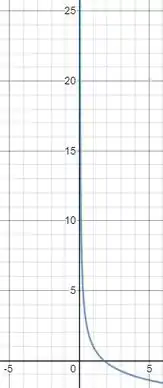
Podemos então, confirmar o que foi encontrado no passo 2: