Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.9 - Ex. 13
Determine o limite:
Passo 1
Bom, queremos saber o limite quando x tende a 1 pela esquerda. . Para isso, vamos apenas observar o gráfico da função:
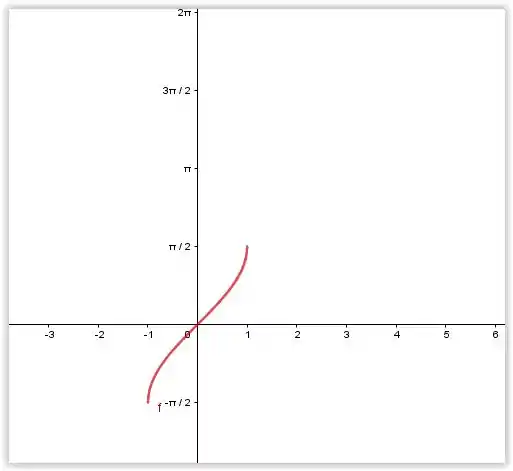
De acordo com a imagem acima, percebemos que quando mais o valor de x ase aproxima de 1 pela esquerda mais o valor do se aproxima do valor
Portanto,
Resposta
Exercícios de Livros Relacionados
Use triângulos de referência como no exemplo 1 para determinar os ângulos nos exercícios abaixo:a) sec - 1 - 2
Use triângulos de referência como no exemplo 1 para determinar os ângulos nos exercícios abaixo:b) cossec - 1 2
Use triângulos de referência como no exemplo 1 para determinar os ângulos nos exercícios abaixo:b) cossec - 1 - 2 / 3
Use triângulos de referência como no exemplo 1 para determinar os ângulos nos exercícios abaixo:a) cotan - 1 - 3 / 3
Provar que:Se y = arccot x , então y ' = - 1 1 + x 2 .