Determine o limite
Passo 1
Sabemos que
Devemos observar que . Logo,
Pelo teorema do confronto, podemos afirmar que
Passo 2
Observando o gráfico, é possível notar que quando a função se aproxima de zero.
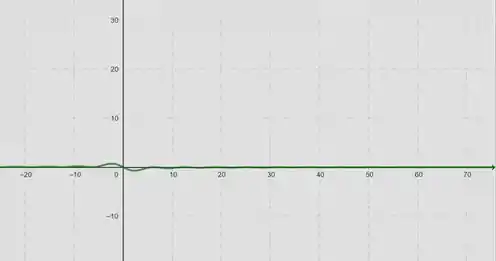
Determine o limite
Sabemos que
Devemos observar que . Logo,
Pelo teorema do confronto, podemos afirmar que
Observando o gráfico, é possível notar que quando a função se aproxima de zero.
