Determine pelo método dos mínimos quadrados a reta que melhor se ajusta aos dados:
b) e
Passo 1
Vamos usar a questão anterior, beleza? Ou seja, resolver aquele sistema, para isso, precisamos encontrar os valores que faltam no sistema abaixo:
Para isso, faremos a seguinte tabela
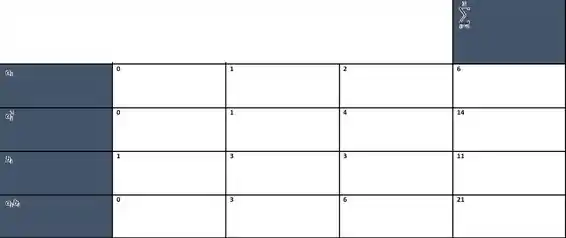
Substituindo no sistema,
Escalonando o sistema acima,
Temos que
E,
Substituindo a equação na função,