Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 18

Determine os momentos de inércia I x , I y , I 0 para a lâmina do Exercício 6 .

Passo 1

Fala turminha, tudo na paz com vocês? Espero que sim! Vamos começar!

Nesse exercício, devemos determinar os momentos de inércia I x , I y , I 0 para a lâmina do Exercício 6 .

Vamos lembrar como era a figura no exercício 6 .

A figura é uma região triangular formada pelas linhas:

y = 0

y = 2 x

x + 2 y = 1

E a densidade é:

ρ x ,   y = x

Temos o seguinte esboço dessa região:

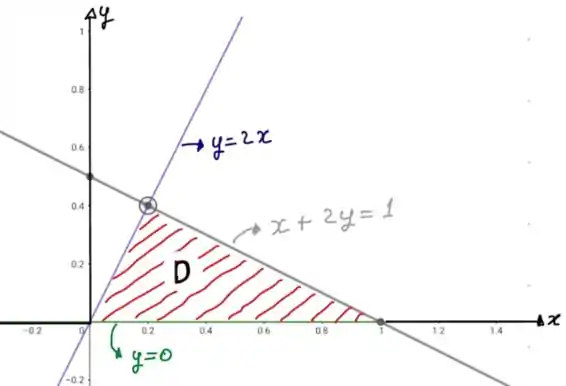
Nossa região de interesse é a região D em vermelho. Olhando para esse gráfico, podemos fazer a seguinte variação dos intervalos de integração:

y 2 ≤ x ≤ 1 - 2 y

0 ≤ y ≤ 2 5

Vale lembrar que calculamos o momento de inércia I x ,   I y   e   I 0 da seguinte forma:

I x = ∬ D   y 2   ρ x ,   y   d A

I y = ∬ D   x 2   ρ x ,   y   d A

I 0 = I x + I y

Precisamos lembrar das relações de coordenadas polares, que são as seguintes:

x = r cos ⁡ θ

y = r   s e n   θ

d A = d x d y = r d r d θ

Com essas informações em mão você pode começar a resolver!

Bora lá!

Passo 2

Vamos começar determinando I x .

Já conhecemos que nossa expressão é:

I x = ∬ D   y 2   ρ x ,   y   d A

Sabemos também que a densidade vale:

ρ x ,   y = x

E os limites de integração são:

y 2 ≤ x ≤ 1 - 2 y

0 ≤ y ≤ 2 5

Substituindo na integral temos:

I x = ∫ 0 2 / 5 ∫ y / 2 1 - 2 y y 2   x   d x d y

Nessa parte tem que ter muito cuidado, pois você deve se lembrar que sempre integramos primeiro os termos que tem funções nos intervalos de integração. No nosso caso, devemos integrar primeiro em d x .

Passo 3

Integrando em d x , ficamos com:

I x = ∫ 0 2 / 5 y 2 x 2 2 y / 2 1 - 2 y d y

Aplicando os limites de integração, vamos ter:

I x = ∫ 0 2 / 5 y 2 ( 1 - 2 y ) 2 2 - ( y / 2 ) 2 2 d y

Simplificando um pouco, ficamos com:

I x = ∫ 0 2 / 5 y 2 1 - 4 y + 4 y 2 2 - y 2 8 d y

I x = ∫ 0 2 / 5 y 2 15 y 2 8 - 2 y + 1 2 d y

I x = ∫ 0 2 / 5 15 y 4 8 - 2 y 3 + 1 2 y 2 d y

Agora integrando em d y , vamos ter:

I x = 3 y 5 8 - y 4 2 + 1 6 y 3 0 2 / 5

Aplicando os limites de integração, temos:

I x = 3 2 5 5 8 - 2 5 4   2 + 1 6 2 5 3  

I x = 12 3125 - 8 625 + 4 375

Logo, nossa resposta é:

I x = 16 9375

Passo 4

Agora vamos determinar I y .

O processo é similar ao que fizemos antes em I x .

Vamos utilizar a formula:

I y = ∬ D   x 2   ρ x ,   y   d A

Substituindo os termos na integral idem ao processo de I x , vamos ter:

I y = ∫ 0 2 / 5 ∫ y / 2 1 - 2 y x 2   x   d x d y

I y = ∫ 0 2 / 5 ∫ y / 2 1 - 2 y x 3   d x d y

Integrando em d x , vamos ter:

I y = ∫ 0 2 / 5 x 4 4 y / 2 1 - 2 y d y

Substituindo os intervalos de integração temos:

I y = ∫ 0 2 / 5 ( 1 - 2 y ) 4 4 - y 2 4   4 d y

Passo 5

Aqui, podemos dar uma simplificada e separar em duas integrais da seguinte forma:

I y = 1 4 ∫ 0 2 / 5 ( 1 - 2 y ) 4 d y - 1 64 ∫ 0 2 / 5 y 4 d y

Na primeira integral, aplicamos uma substituição do tipo:

u = 1 - 2 y

- d u 2 = d y

Substituindo na integral, temos:

I y = 1 4 ∫ 0 2 / 5 u 4 - d u 2 - 1 64 ∫ 0 2 / 5 y 4 d y

Integrando e voltando para a variável y temos:

I y = - 1 8 ( 1 - 2 y ) 5 5 - 1 64 y 5 5 0 2 / 5

Aplicando os limites de integração, vamos ter:

I y = - 1 8 ( 1 - 2 2 5 ) 5 5 - 1 64 2 5 5 5 - - 1 8 1 - 2 0 5 5 - 1 64 0 5 5

Simplificando vamos ter:

I y = - 1 8 1 3125 5 - 1 64 32 3125 5 + 1 40

I y = - 1 125000 - 1 31250 + 1 40

Logo, o valor de I y é:

I y = 78 3125

Passo 6

Por fim, para determinarmos o valor de I 0 aplicamos a relação:

I 0 = I x + I y

Como:

I x = 16 9375

I y = 78 3125

Substituindo na formula, vamos ter:

I 0 = 16 9375 + 78 3125

Somando, temos que I 0 vai valer:

I 0 = 2 75

Resposta

I x = 16 9375

I y = 78 3125

I 0 = 2 75

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma lâmina que ocupa, no primeiro quadrante, a região D limitada pela parábola x = 1 - y 2 e pelos eixos coordenados, com função densidade �� x , y = y .�� a Determine a massa da lâmina. ( b
Determine os momentos de inércia I x , I y , I 0 para a lâmina do Exercício 3 .
Centroide de um bumerangue Encontre o centroideda regiao em forma de bumerangue entre as parábolas y 2 = - 4 x - 1ey 2 = - 2 ( x - 2 ) no plano xy.
Inércia polar de uma placa triangular Encontre o momento de inercia polar em relacao a origem de uma placa triangular fina de densidade constante δ = 3 delimitada pelo eixo y e as retas y = 2x e y = 4
Massa e inércia polar de um contrapeso O contrapeso de um volante de densidade constante 1 tem a forma da parte menor cortada de um circulo de raio a por uma corda a uma distancia b do centro (b a). E