Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 17

Determine onde e é a curva obtida como intersecção das superfícies de equações , e , orientada no sentido de crescimento de .

Passo 1

Faala Zezé, bom dia cara.... Vamos para mais uma questãozinha que envolve Teorema de Stokes.

De lei, de praxe, como sempre, vamos tentar esboçar as superfícies pra ver se conseguimos enxergar a nossa curva:

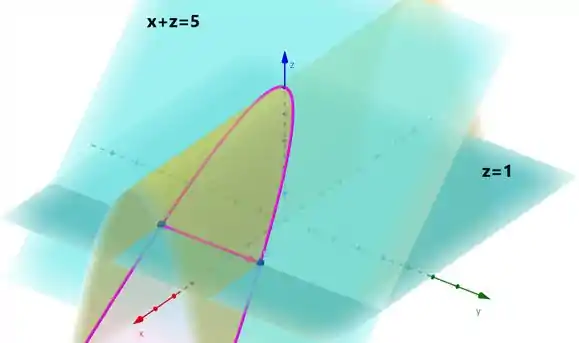
Teremos algo mais ou menos assim; a parte que nos interessa é a intersecção da superfície em amarelo com o plano , tomando . Vamos pegar só a superfície que nos interessa, já colocando a orientação no sentido crescente de :

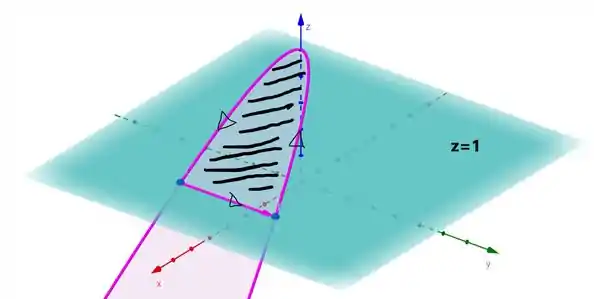
É aquela superfície que nos interessa. Repara que temos dois pontos ali, que podem ser encontrados; sabendo que estão sob o plano , basta substiruirmos:

Portanto,

Então encontramos: e .

Guarda essas informações aí porque elas podem ser úteis.

Passo 2

Bom, O que o exercício quer é que calculemos o seguinte:

Onde a curva é só a BORDA da superfície que achamos, ou seja, é só a parte em rosa.

Essa integral pode ficar mais fácil se aplicarmos o teorema de Stokes; isso significa transformar essa integral de linha em uma integral de superfície. Teremos:

Agora, essa superfície é exatamente a superfície hachurada cuja borda esta em rosa.

Bom, vamos encontrar então o rotacional desse campo; lembrando que:

Assusta! Mas é bem tranquilo. Sabendo que:

Então tudo que precisamos fazer é derivar esses termos aí:

Puts grila...

O que isso significa?? Basicamente isso está dizendo duas coisas pra gente:

Que o é um campo Gradiente; ou seja, existe uma função tal que:

O campo é conservativo; isso significa que não importa o caminho que ele percorre, somente os pontos de partida e de chegada:

Bom, então para resolver o exercício vamos ter que encontrar essa tal e aplicar os pontos e nela.

Passo 3

Mas como? Vamos invocar o item (i) ali em cima; ao nos dizer que é gradiente de , ele ta dizendo o seguinte:

Entendeu a idéia?? Isso significa que se integrando isso podemos encontrar uma . Bora fazer isso logo então:

Integrando:

Obtemos:

Opa, da onde saiu aquele ?? Ele nada mais é do que um termo que representa a possibilidade de existir algo em função somente de e ; quando derivamos sob , esse termo é dito constante e então some.

Se a gente assumir que aquele ali é mesmo a verdadeira forma dessa função, ao derivarmos em relação a esperamos obter . Vamos ver se isso é verdade:

Mas isso teria que ser igual a:

Isso só será verdade se:

Integrando isso:

Denovo estamos admitindo a existência de algo somente em função de , de forma que se derivamos em função de esse termo desaparece.

Então até agora nossa função tem a seguinte forma:

Para comprovar a existência desse termo, vamos derivar essa em função de :

Esperamos que isso seja igual a :

Isso será verdade, se:

Integrando:

Portanto:

E finalmente encontramos uma forma para :

Mas carmeia que ainda não é essa a resposta. Precisamos aplicar os ponto A e B nessa função:

Então o resultado da nossa integral:

É isso!!

Resposta

Concluindo:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∬ S r o tF ⋅ n d s , onde F x , y , z = ( y , 2 x , x y z ) e S é a superfície lateral da pirâmide da figura 7.24 com normal n exterior a S .

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva C . ∮ C yd x + z d y + x d z = - 2 π 2 Onde C é a curva obtida como i

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva C . ∮ C 3 y + z d x + x + 4 y d y + 2 x + y d z = - 3 2 π a 2 4 Onde

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando em cada caso, a orientação da curva C . ∮ C ( 2 x yd x + 1 - y z + x 2 + x d y + x 2 2 + e z d z = π Onde