Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 2
Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando, em cada caso, a orientação da curva .
Onde é a curva obtida como interseção da esfera com o plano .
Passo 1
Eaaeee... mais uma questãozinha para aplicarmos Stokes. Vamos juntos!
Rotina já, tentar esboçar a esfera e o plano pra enxergar onde esta a curva:
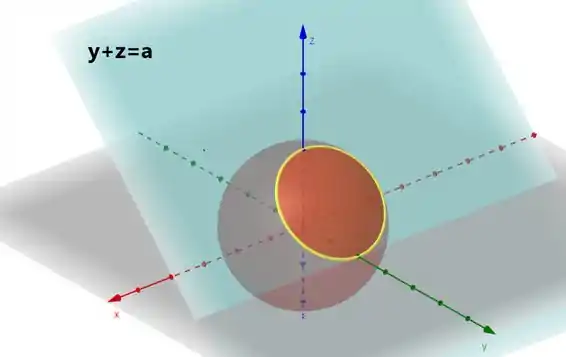
Teremos algo parecido com isso. Vamos agora isolar a nossa queridinha curva:
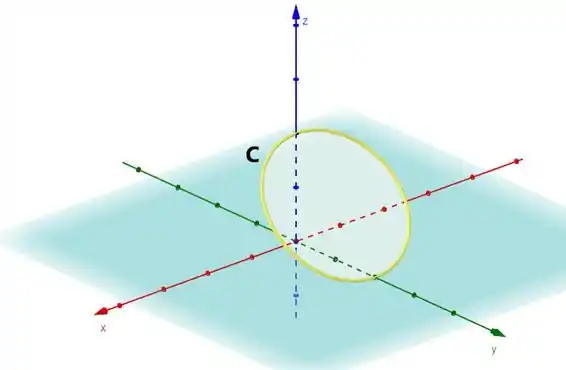
Beleza! Essa é a cujo dita, tal que:
Para demonstrar se esse resultado aí é verdade ou não, vamos aplicar Stokes:
Só que o teorema não trabalha mais sob a curva, ele funciona sob uma superfície fechada, cuja borda seja a curva . Em outras palavras, uma das possibilidades de superfície é:
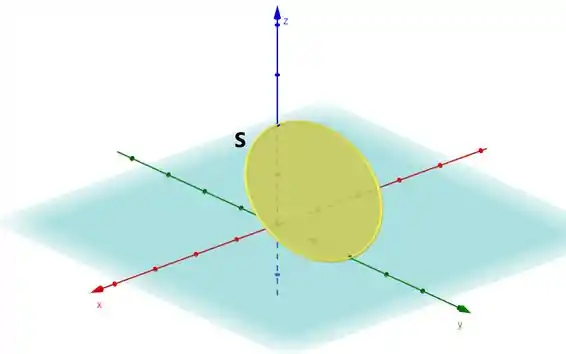
A diferença é sutíl.. mas é importante saber.
Superficie ta Ok; vamos atrás dos outros caras que tão dentro da integral. Bora!
Passo 2
Vamo começar com o rotacional. Lembrando que o nosso campo nesse exercício foi dado por:
E não podemos esquecer nunca que o rotacional é obtido assim:
Então tudo que precisamos fazer é encontrar essas derivadas parciais:
E
Portanto nosso rotacional será:
Tranquilo demais até aqui né?!
Agora a próxima criatura que devemos achar é o vetor normal. Repare que o vetor normal à nossa superfície nada mais é do que o vetor normal ao plano .
Vê se na imagem fica claro:
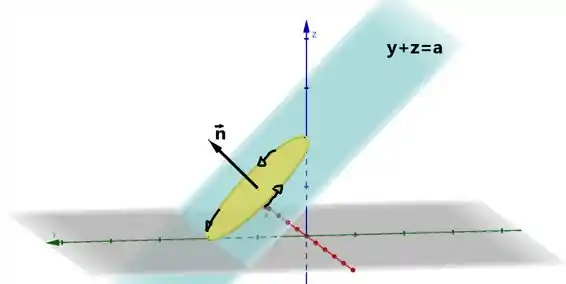
Repare que, além do vetor ser normal ao plano, tomamos a orientação da curva como sendo no sentido anti-horário. E definindo isso percebemos que o vetor normal está meio que apontado para a nossa esquerda.
OBS: Lembra como encontra isso? Com a mão direita coloca ela na tela; faz o sinal de “jóia” , com os outros 4 dedos você percorre a curva no sentido que definimos, ou seja, faça com que os seus dedos tentem entrar na tela. Percebeu que seu dedão ta apontando pra esquerda e um bocado inclinado? É o sentido do nosso vetor.
Então tá, ele é mesmo normal ao plano. Agora você lembra que num plano genérico qualquer:
O vetor normal à ele será: .
Portanto trazendo isso pro nosso pobleminha:
Então já temos o seguinte:
Passo 3
No final das contas sobrou pra gente encontrar aquela integralzinha ali. Repare que ela representa a area de uma curva:
Portanto, devemos projetar a nossa superfície no plano. Optando pelo plano , teremos o seguinte:
Pegou a ideia?? Então no final das contas o que queremos é a area dessa elipse.
Mas vamos quem é essa elipse?? Precisamos saber a forma matemática dela; basta então tomar a interseção, olha só:
Como escolhemos o plano temos que definir ela somente em termos desses caras:
Dividindo por 2:
Temos que fazer isso nos lembrar a equação de uma elipse, certo? Uma das forma é somando o termo em ambos os lados da igualdade:
Repare que:
Então:
E como na equação da elipse sempre deixamos o após o igual:
Agora, lembra que a area de uma elipse é quase igual a de uma circunferência, com o detalhe de que na elipse temos “dois” raios (nunca diga isso pro seu professor; acho que ele não vai curtir muito. Mas é uma boa forma de lembrar)
Então:
Ta quase parecido com o resultado que o enunciado pediu, se racionalizarmos:
Lembrando ainda que tínhamos um (-3) né?!
Portanto:
Exatamente como queríamos demonstrar.
Resposta
Mostramos ser verdade que: