Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 3

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando em cada caso, a orientação da curva C .

∮ C ( 2 x y   d x + 1 - y z + x 2 + x d y + x 2 2 + e z d z = π

Onde C é a curva obtida como intersecção do cilindro x 2 + y 2 = 1 ,     z ≥ 0 , com o cone z 2 = x 2 + y - 1 2 .

Passo 1

Faalaa joooveeenss...Vamos para mais uma questãozinha de Teorema de Stokes. Bora lá!

Como já é de praxe, vamos tentar enxergar quem é a nossa curva C :

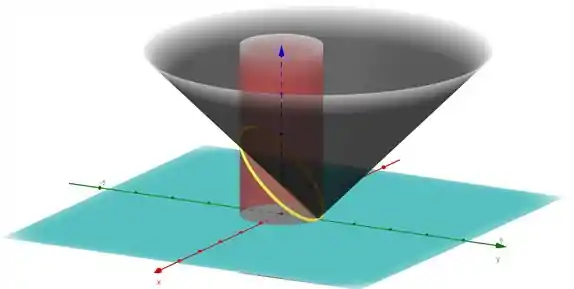
Teremos algo mais ou menos assim. Consegue perceber que a nossa curva C será algo assim se isolarmos ela:

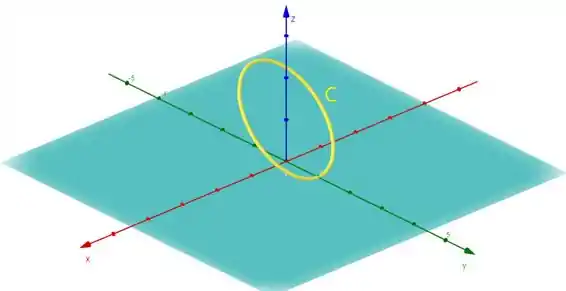
Beleza então de acordo com o exercício, temos:

∮ C F →     d r = π

O que precisamos fazer é provar isso usando Stokes; lembrando que o teorema diz o seguinte:

∮ C F →   d r   = ∬ S r o t F →   .     n →   d s = ∬ S r o t F →     .     N →   d x d y  

Tudo que precisamos fazer é ver se essa integral sob a SUPERFÍCIE S é igual a π .

Então antes de calcular o rotacional e tudo mais, vamos definir quem é a nossa superfície; a forma mais simples dela será:

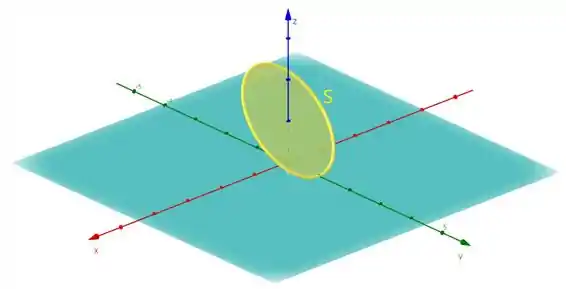
Consegue notar a diferença?? É muito importante saber essa “diferença” entre a curva C e a superfície S .

Passo 2

Top. Então com a nossa S definida, vamos começar a encontrar os carinhas que compõem nossa integral.

Começando pelo Rotacional; lembra dele?? É mais ou menos assim:

r o t F → = ∇   x   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3 = ∂ F 3 ∂ y - ∂ F 2 ∂ z   ;   ∂ F 1 ∂ z - ∂ F 3 ∂ x     ;   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Onde:

F x , y , z = 2 x y ⏟ F 1   ;   1 - y z + x 2 + x ⏟ F 2   ;   x 2 2 + e z ⏟ F 3

Então bora lá:

∂ F 3 ∂ y - ∂ F 2 ∂ z = 0 - 1 - y = y - 1

∂ F 1 ∂ z - ∂ F 3 ∂ x = 0 - x = - x

E

∂ F 2 ∂ x - ∂ F 1 ∂ y = 2 x + 1 - 2 x = 1

No final das contas, o nosso rotacional será:

r o t F → = y - 1     ;   - x   ;     1

Agora o vetor normal; ele é normal a parede do cone, certo?

Ou seja, parametrizando isso:

z = x 2 + y - 1 2

Teremos o seguinte:

f x , y = ∂ f ∂ x ; ∂ f ∂ y ; 1

Lembrou??

Então resolvendo essas derivadas:

∂ f ∂ x = 1 2 2 x x 2 + y - 1 2 1 2 - 1 = x x 2 + y - 1 2

E

∂ f ∂ y = y - 1 x 2 + y - 1 2

Passo 3

Portanto nosso vetor normal:

n → = x x 2 + y - 1 2   ;   y - 1 x 2 + y - 1 2   ; 1

Então a nossa imtegral:

∬ D y - 1   ;   - x     ; 1   .   x x 2 + y - 1 2   ;   y - 1 x 2 + y - 1 2   ; 1   d x d y

Aí olhando aquele troço do enunciado e esse agora só podemos chegar a uma conclusão:

Pois é. Mas repara só uma coisa, fazendo o produto vetorial:

∬ D x y - 1 x 2 + y - 2 2 - x y - 1 x 2 + y - 1 2 + 1   d x d y

Aqueles dois termos se anulam. E aí fica fácil demais:

∬ D d x d y = A r e a  

Ou seja, isso deverá ser a area da projeção ( D ) da nossa superfície no plano x y :

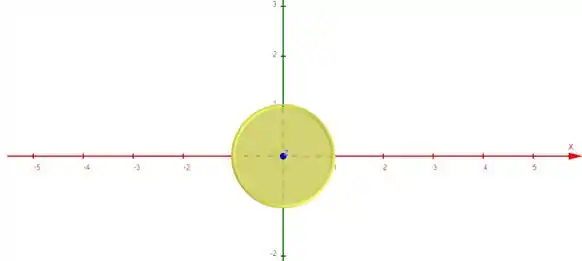
Teremos uma circunferência de raio 1 no plano x y .

Portanto o resultado da nossa integral nada mais é do que a area dessa circunferência:

∬ D d x d y = A = π 1 2 = π

Resposta

Provamos então, que:

∮ C F →   d r = ∬ S r o t F → .   n →   d s = π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F um campo vetorial diferenciável definido em uma região contendo uma superfície orientada fechada e lisa S e seu interior. Seja n o campo vetorial normal unitário em S. Suponha que S seja a uniã
Seja n a normal unitária exterior da casca elíptica S : 4 x 2 + 9 y 2 + 36 z 2 = 36 ,z ≥ 0 E seja F = y i + x 2 j + x 2 + y 2 3 / 2 sen ⁡ e x y z k Encontre o valor de ∬ ∇ × F ∙ n d σ (Sugestão: uma p
Nos Exercícios 13-18, utilize a integral de superfície no teorema de Stokes para calcular o fluxo do rotacional do campo F através da superfície S na direção da normal unitária exterior n .15. F = x 2
Seja n a normal unitária exterior (normal para longe da origem) da casca parabólica S : 4 x 2 + y + z 2 = 4 , y ≥ 0 E seja F = - z + 1 2 + x i + t g - 1 y j + x + 1 4 + z k Encontre o valor ∬ ∇ × F ∙
Nos Exercícios 13-18, utilize a integral de superfície no teorema de Stokes para calcular o fluxo do rotacional do campo F através da superfície S na direção da normal unitária exterior n .13. F = 2 z