Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 73
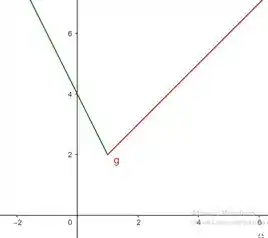
Determine os pontos críticos,extremidades de domínio e valores extremos (absolutos e locais) da função:
Passo 1
Para encontrarmos o(s) ponto(s) crítico(s), precisamos derivar as equações.
Passo 2
Derivando as equações separadamente, temos:
Passo 3
Igualando ambas as equações, teremos o ponto em que elas se encontram:
Passo 4
Como podemos inclusive conferir no gráfico.
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da