Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 20
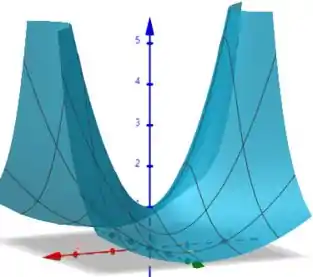
Determine, com precisão de quatro casas decimais, a área da parte da superfície que está acima do quadrado . Ilustre, traçando o gráfico da superfície.
Passo 1
Para resolver esse problema, vamos utilizar a definição para calcular a área da superfície e após isso, vamos utilizar um software para resolver a integral final.
Passo 2
Queremos calcular a seguinte integral:
Primeiro, vamos encontrar e . Fazendo a primeira derivada parcial, temos que
Agora para a outra derivada, temos que
Manipulando nosso domínio , temos que o intervalo de integração, mantendo fixo e variando , será
Substituindo na integral todos os valores obtidos e usando um software para o cálculo numérico, chegaremos no resultado de
Sendo que nossa superfície será
Resposta
Exercícios de Livros Relacionados
Determine a área da superfície.A parte da esfera x 2 + y 2 + z 2 = 4 que está acima do plano z = 1 .
Se você tentar utilizar a Fórmula 2 para determinar a área do topo superior da esfera x 2 + y 2 + z 2 = a 2 , terá problemas, porque a integral dupla é impropria. De fato, o integrando tem uma descont
Determine a área da superfície.A parte da esfera x 2+ y 2+ z 2= 4 z que está dentro do parabolóide z =x 2 + y 2 .
Determine a área da superfície.A parte da esfera x 2+ y 2+ z 2= a 2 que está dentro do cilindro x 2 + y 2 = a x e acima do plano x y .
Determine a área exata da superfície z = 1 + 2 x + 3 y + 4 y^2 , 1 = x = 4 , 0 = y = 1 .