Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 18
Determine a área exata da superfície
, ,
Passo 1
E aii, belezinha?
Nessa questão vamos precisar calcular a área de uma superfície do tipo .
Pra calcular isso, usamos a fórmula:
Onde é o domínio do gráfico que gera .
A gente vai começar pegando esse pra calcular as derivadas parciais.
Dai, montamos a integral dessa fórmula, e com o domínio transformamos ela em uma integral iterada.
Por último, vamos usar um software (no caso, o WolframAlpha) pra definir o valor dessa integral.
Passo 2
A equação que define a superfície é:
Então essa vai ser nossa função :
As derivadas parciais nós calculamos mantendo uma variável como constante e derivando em função da outra.
Primeiro em função de :
Agora em função de :
Vamos colocar isso na fórmula:
Então:
Passo 3
O domínio de integração é:
Então a integral iterada fica assim:
Agora vamos colocar essa integral no WolframAlpha:
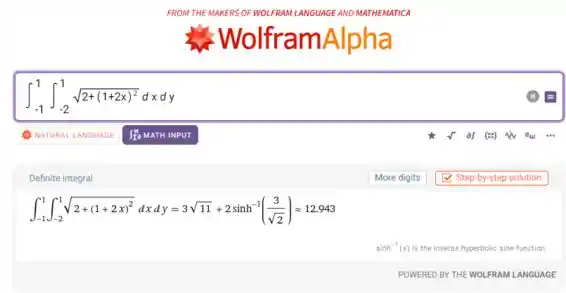
é a função inversa do seno hiperbólico – chamamos de arco seno hiperbólico ().
Então: