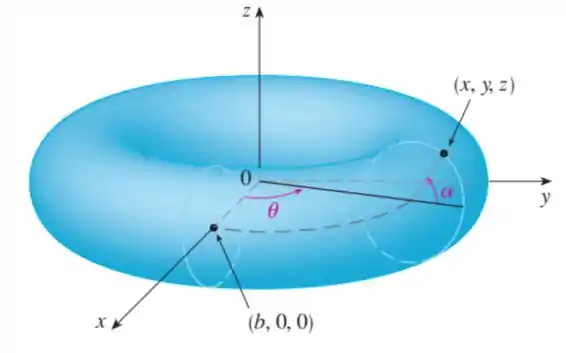
(a) Determine a representação paramétrica do toro obtido girando em torno do eixo o círculo do plano com centro em e raio . [Sugestão: tome como parâmetros os ângulos e mostrados na figura.]
(b) Use as equações paramétricas encontradas na parte (a) para traçar o gráfico do toro para diversos valores de e .
(c) Use a representação paramétrica da parte (a) para achar a área do toro.
Passo 1
E aê, gente legal. Tudo belezal? 😊
No item (a), precisamos determinar os parâmetros da figura do enunciado chamada de toro (nome engraçado, né?) obtido quando está girando em torno do eixo o círculo do plano
com centro em e raio .

No item (b), precisamos fazer o gráfico desse toro usando os novos parâmetros encontrados em (a), com valores diversos para e .
E no item (c), encontrar a área de superfície para esse toro. Socorro, né? Mas calma e vamos lá 😊
Passo 2
(a) Vamos observar a seguinte figura:
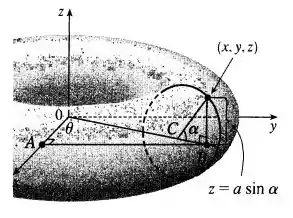
Vamos pensar: o que aconteceria quando girarmos o ponto em relação a ?
Vamos considerar uma parametrização do círculo no plano com centro e o raio para as coordenadas polares:
Agora, e se rotacionarmos o círculo sobre o eixo para obter um toro?
A rotação pode ser representada por um ângulo no plano . As novas coordenadas e depois dessa rotação podem ser, respectivamente:
A coordenada é a mesma de antes da rotação. Logo, podemos fazer a parametrização do toro como
Onde
Passo 3
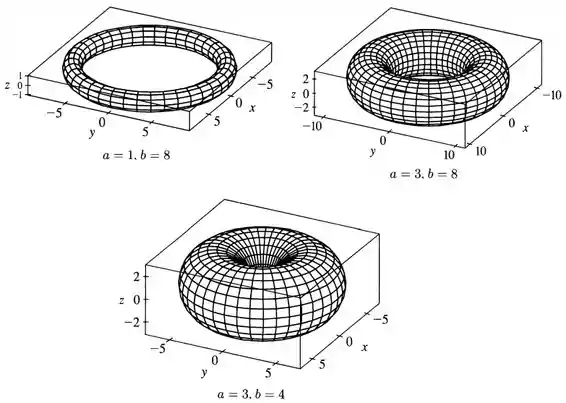
(b) Agora vamos chutar alguns valores de e nas equações paramétricas já encontradas para traçar gráficos de toros.
Passo 4
(c) Vamos agora encontrar a área da superfície desse toro.
Onde precisamos calcular o módulo do produto vetorial das derivadas parciais da representação paramétrica da superfície. Socorroo... Calma lá.
De acordo com a nossa parametrização, temos:
Derivando em relação a e a , obtemos:
Agora tomemos o produto vetorial:
Resolvendo, chegaremos a
Portanto, seu módulo será igual a:
Passo 5
Show! Agora podemos escrever a integral e resolvê-la, a fim de achar a área da superfície do toro:
Reorganiznado a integral, podemos calcular por partes:
Substituindo os limites de integração, teremos:
Resposta