Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.1 - Ex. 53
Determine se a sequência converge ou diverge. Se ela convergir, encontre o limite.
Passo 1
Hey, galera! Nessa questão queremos determinar se a sequência do enunciado diverge ou converge, certo?
Lembrando que nossa sequência é
Aqui não temos uma fórmula geral de pra tentar calcular o limite, então temos que observar o padrão dos primeiros termos.
Passo 2
Parece que os vão ficando cada vez mais espaçados, e isso poderia acabar nos sugerindo a ideia de que os predominariam sobre os , e a sequência convergiria pra . Mas isso é falso! Por que??
Pode ter zeros seguidos, mas se ainda tiver um único depois desses zeros, ainda não podemos falar que converge pra . Plotando o gráfico dessa sequência, teremos
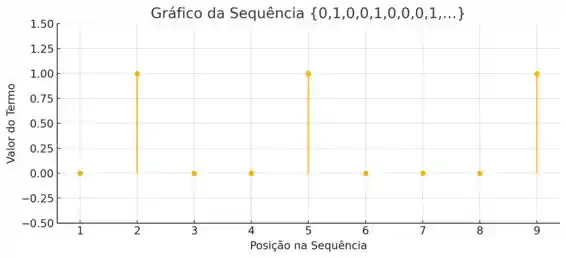
Ou seja, sequência não está se aproximando de um único número, pois os 1s continuam a aparecer e o número de zeros entre eles está aumentando indefinidamente. Portanto, a sequência diverge!
Resposta
Sequência divergente