Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 73
Use a tabela de valores de para estimar os valores de , e .
Passo 1
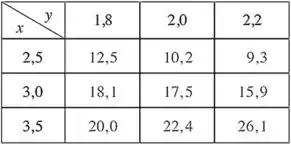
Show de bola, galera! Precisamos ver como vamos fazer pra estimar aquelas derivadas parciais do enunciado... Vamos retomar a tabela com os valores da função :
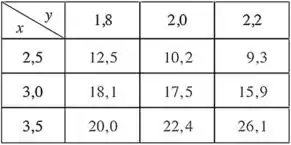
A questão quer que a gente estime a derivada parcial da função em três pontos dados
Primeiro, vamos entender como estimar a derivada para um certo ponto, depois repetimos o procedimento para os outros, beleza?
Passo 2
Começando por
A ideia geral consiste em usar a definição de derivada parcial.
Se temos uma função e queremos calcular a derivada de com relação a , nós temos que deixar a variável fixa e fazer pequenas variações em torno do valor de
Matemáticamente, escrevemos:
Na nossa tabela, para um valor fixo de só há dois valores possíveis de para fazermos essa variação.
Por exemplo, para o ponto fixamos e variamos . A menor variação possível para é . Com essa variação, estimaremos a derivada com relação a utilizando também os pontos e .
Vamos fazer o seguinte:
A derivada será a média dessas estimativas:
Depois disso, vamos repetir a dose para , ou seja:
Por último, vamos aproveitar essas 2 primeiras estimativas de e de para calcular a seguinte estimativa:
Vamos às contas agora!
Passo 3
Vamos às contas começando por
Então,
Passo 4
Agora vamos calcular
Assiiimm....
Passo 5
Por fim, podemos calcular