Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.3 - Ex. 64
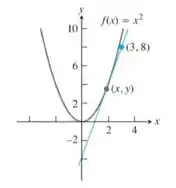
Determine todos os pontos no gráfico de com tangentes que passam pelo ponto .
Passo 1
A primeira coisa que precisamos fazer é encontrar a equação da reta tangente à curva . Para isso, precisamos achar o coeficiente angular da reta.
Passo 2
Lembrando que a equação da reta tangente é:
Substituindo o coeficiente angular na equação da tangente
Passo 3
Substituindo o ponto na equação da tangente:
Como o ponto é o ponto tangencial, esse ponto pertence a tangente e a curva . Logo,
Igualando,
Utilizando Bhaskara,
Assim,
Passo 4
Já que achamos os valores de , agora precisamos achar os valores de :
Pronto!!!
Resposta
Exercícios de Livros Relacionados
Calcule a derivada. f x = ln cos x 1 + sen x
Calcule a derivada. g x = e sec x x
Calcule a derivada. y = ln 1 - x + 1 + x 1 - x - 1 + x - 1 - x 2 x
Calcule a derivada. y = e - 3 x cos 3 x - sen 3 x
Calcule o limite: lim x → - π / 6 1 + cos π ⋅ c o s s e c x