Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.4 - Ex. 4
Determine o valor máximo de onde e estão sujeitos a ,
Passo 1
Perceba que não tem ponto crítico.
Vamos analisar a fronteira.
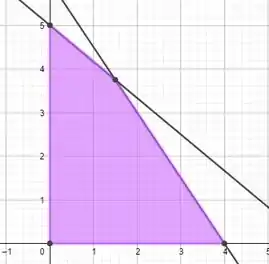
Temos os pontos . Aplicando a função,
E
E,
E
Sendo assim, é máximo
Resposta
é máximo
Exercícios de Livros Relacionados
Encontre os valores máximo e mínimo absoluto de f na região D . f x , y = x 2 + y 2 + x 2 y + 4 d = x , y x ≤ 1 ,y ≤ 1 }
Determine os valores máximo e mínimo absolutos de f no conjunto D .33. f x , y = x 4 + y 4 - 4 x y + 2 . D = { ( x , y ) | 0 ≤ x ≤ 3 ,0 ≤ y ≤ 2 }
Determine os valores máximo e mínimo absolutos de f no conjunto D . f x , y = x y 2 , D = x , y x ≥ 0 , y ≥ 0 ,x 2 + y 2 ≤ 3
Determine os valores máximos e mínimo absolutos de f no conjunto D. f x , y = 3 + y x - x - 2 y , D é a região triangular fechada com vértices 1 , 0 ,5 , 0e1 , 4