Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 31
Encontre os valores máximo e mínimo absoluto de na região .
Passo 1
Oie, vamos de resolução hoje.
Aqui a gente tem a função:
Neste exercício, precisamos encontrar e classificar os pontos críticos da função.
Para determinar os valores máximo e mínimo absolutos de uma função contínua em um conjunto fechado e limitado :
1. Determine os valores de nos pontos críticos de em .
2. Determine os valores extremos de na fronteira de .
3. O maior dos valores dos passos e é o valor máximo absoluto; o menor desses valores é o valor mínimo absoluto
Como é um polinômio e é contínuo em , afirmamos que existe máximo e mínimo absoluto, em que é a região quadricular fechada, com vértices
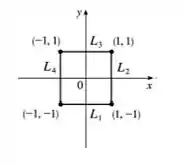
Passo 2
Vamos encontrar então as derivadas parciais:
Primeiro iremos encontrar a derivada parcial em relação a :
E agora iremos calcular em relação a :
Os pontos críticos:
nos dá como o único ponto crítico em , com
Passo 3
Agora vamos analisar cada lado do quadrado:
Em
E
Temos então:
é uma constante.
Em
e
uma função quadrática em que possui máximos e mínimos nos extremos do intervalo do lado , que é :
e mínimo
Em
que possui máximo em
e
com
e mínimo em
Em
que possui máximos e mínimos nos extremos do intervalo do lado , que é :
e mínimo em
Assim, os máximos absolutos são em são e o mínimo absoluto em com
Resposta
Os máximos absolutos são em são e o mínimo absoluto em com