Determine os valores máximos e mínimo absolutos de no conjunto D.
D é a região triangular fechada com vértices
Passo 1
Oi, galerinha! Tudo bom?
Dada a função:
A gente quer encontrar os valores máximos e mínimos absolutos dessa função dentro do conjunto D que vocês irão ver logo abaixo, num gráfico.
Como é um polinômio e é contínuo em , afirmamos que existe máximo e mínimo absoluto, em que é a região triangular fechada, com vértices
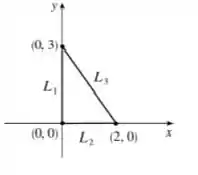
Veja que temos então lados aqui, que é dado por , que é dado por e que é dado por .
Vamos calcular as derivadas parciais, resolver o sistema das equações para encontrar os valores de e para o ponto critico. Em seguida, encontraremos os valores máximos e mínimos no limite de e comparar seus valores.
Bora lá!
Passo 2
O enunciado forneceu,
Então temos que,
e
Veja que não temos pontos críticos, já que as derivadas parciais não possuem zeros.
Deveremos então substituir os valores
Em e observar o seu comportamento.
Para , não varia, apenas .
Então temos que em :
e
para
Como a função é decrescente em o valor máximo é e o mínimo é .
Agora vamos aplicar o mesmo para e .
Passo 3
Em
e
para
Como a função é crescente em , o valor é mínimo é e o máximo é
Em
e
Como a função é crescente em , o valor mínimo é
e o máximo é
Assim, o máximo absoluto de em é e o mínimo absoluto é
Resposta
O máximo absoluto de em é e o mínimo absoluto é