Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 16
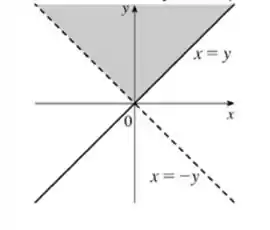
Determine e faça o esboço do domínio da função.
Passo 1
Eaeee, belezinha?? Bom... o enuciado nos deu a seguinte função:
Queremos determinar o domínio de .
Ou seja, queremos saber que valores de que podem ser usados para que seja real.
Para definir o domínio, é melhor olhar para as restrições que impossibilitam a função ter um valor real (divisão por zero, raízes de números negativos, logaritmos de números não positivos).
Agora bora lá!! 😉
Passo 2
Da nossa função, temos:
Temos duas restrições aqui: A raiz quadrada deve ter um radicando maior que zero e o logaritmo deve ser de um número maior que zero, ou seja:
E
Juntando as duas confições, temos a seguinte condição.
Logo, o nosso domínio são todos os números reais dentro desse intervalo, ou seja:
Com isso, ppodemos plotar o domínio da nossa função (região hachurada):
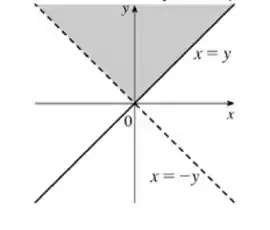
Resposta
