Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 50
Um prédio retangular está sendo projetado para minimizar a perda de calor. As paredes leste e oeste perdem calor a uma taxa de por dia, as paredes norte e sul, a uma taxa de por dia, o piso, a uma taxa de por dia e o teto, a uma taxa de por dia. Cada parede deve ter pelo menos de comprimento, a altura deve ser no mínimo , e o volume, exatamente .
- Determine e esboce o domínio da perda de calor como uma função dos comprimentos dos lados.
- Encontre as dimensões que minimizam a perda de calor. (Analise tanto os pontos críticos como os pontos sobre a fronteira do domínio.)
- Você poderia projetar um prédio com precisamente menos perda de calor ainda se as restrições sobre os comprimentos das paredes fossem removidas?
Passo 1
Galera, nessa questão nós temos informações sobre a taxa de perda de calor das paredes, do piso e do teto de um prédio. Além disso, sabemos que cada parede deve ter pelo menos de comprimento e altura de, no mínimo,, bem como um volume de .
Pensando no prédio como uma caixa retangular de lados , sabemos que o seu volume será
Pela restrição imposta ao volume, teremos
Logo,
Precisamos determinar o domínio da função que dá a perda de calor do prédio. Primeiro vamos escrever uma equação para o calor perdido (usando as taxas fornecidas no enunciado), olha só:
Assim,
Substituindo na equação de cima , temos:
Com essa função da perda de calor em função das dimensões nós podemos esboçar domínio, encontrar o ponto crítico que minimiza a perda de calor e o volume do prédio no caso de mínima perda de calor.
Vamos lá...
Passo 2
a) O enunciado nos disse que a altura que a altura deve ser maior que 4. Logo,
Então,
E isso implica em:
Como cada parede deve ter pelo menos de comprimento, ou seja:
e
Logo,
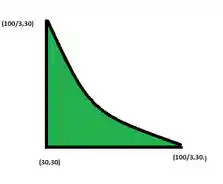
Nessa região temos a reta vertical definida por , a reta horizontal definida por , bem como a curva onde . Nossa região é a região de dentro dessas curvas, incluindo as fronteiras.
Passo 3
b) Como queremos saber as dimensões que minimizam a perda de calor, a ideia vai ser achar , e igualar a zero para achar os pontos críticos. Em seguida, veremos os pontos de mínimo.
Derivando em relação a :
Em relação a :
Igualando a a zero:
Logo,
Fazendo o mesmo com :
Usando a relação :
Fazendo as contas, temos:
Portanto,
Assim, o único ponto crítico de seria , porém este não pertence a
Passo 4
Como o ponto crítico não pertence a , vamos olhar a fronteira de . Analisando:
Em
Derivando,
Como , nossa função é crescente nesse intervalo e possuirá seu ponto de mínimo quando e máximo em . Calculando o nesses pontos, temos:
e
Em :
Derivando,
No intervalo nossa função é decrescente e possuirá ponto de mínimo em e máximo em . Assim,
e
Em
Derivando,
No intervalo será positivo e, assim, será crescente de com ponto de mínimo em e máximo em .
e
Logo, o mínimo absoluto de será:
Então, as dimensões do muro ficam o seguinte:
e
Como :
Logo,
Passo 5
c) Pelo item (b) vemos que o único ponto crítico de era . Como :
Portanto,
, e
Resposta
- O mínimo absoluto de é e as dimensões dos muros são , e
- , e