Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 34
Outro modelo razoável para a velocidade escalar da água do rio no exercício 33 é a função senoidal . Se o piloto do barco quiser atravessar o rio de A até B com direção constante e velocidade escalar constante de , determine o ângulo no qual o barco deve seguir.
Passo 1
Resumindo os dados da questão 33:
Tínhamos uma porção reta em um rio onde a água percorria em velocidades altas no meio, porém velocidades quase nulas perto das margens.
Nessa questão isso é descrito pela função .
O piloto quer fazer o percurso, saindo de A e chegando em B (trajeto esse de 40 metros), com velocidade escalar e direção constante.
Basicamente ele vai mirar o barco em um ângulo específico (para compensar a velocidade da água que empurra ele para a outra direção) e prosseguir com velocidade constante.
Talvez a imagem abaixo ajude a visualizar:
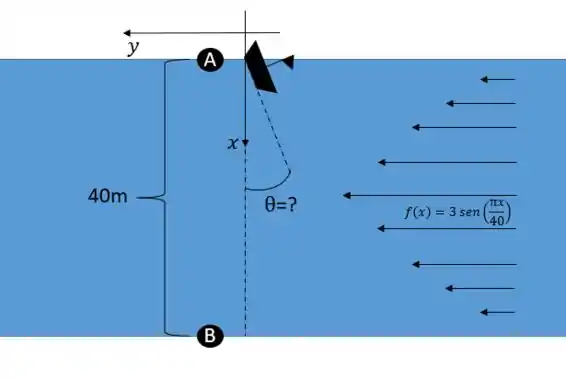
Para essa questão, a gente vai modelar essa situação até encontrar uma equação em que seja nossa única variável. Aí é só isolar e passar pra próxima.
Passo 2
Sejam os eixos posicionados tal qual a figura e com origem no ponto A, finalmente podemos modelar a situação.
Sabemos que:
Mas além disso, na componente da velocidade do barco, também é preciso considerar a velocidade da água. E como velocidade nada mais é que a derivada da posição em relação ao tempo, teremos o seguinte sistema:
Da primeira equação, tiramos que , enquanto na segunda temos
Assim,
Integrando essa equação, obtemos uma expressão para o movimento do barco em que depende apenas do tempo e do ângulo.
Passo 3
Com a expressão que temos, precisamos eliminar as variáveis extras ( e ) e isolar o valor de .
O tempo necessário para a travessia ocorre para , de modo que, ao substituir na expressão de que encontramos anteriormente, temos:
Assim, substituindo na expressão para :
Como substituímos o valor do tempo no momento que o barco chega no ponto B, agora nós temos uma expressão que mostra a posição em do barco nesse momento.
Mas veja bem, quando o barco chega no ponto B ele está de volta em !!!! (Conforme a origem que nós definimos).
Assim, só precisamos substituir o valor de nessa última expressão e encontrar o tal do .
Então por fim, o ângulo de partida do barco foi:
Ou ainda
Obs.: O sinal negativo aqui é por causa dos eixos que a gente definiu lá na figura. Se tivéssemos invertido o eixo o sinal serial positivo.