Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 4
Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de t especificados.
Passo 1
Fala ai, belezinha?
Nesta questão vamos precisar determinar algumas grandezas, tais como a velocidade e aceleração. E para isso, basta derivarmos a posição.
Se liga! Para a velocidade derivamos a posição uma vez e para a aceleração derivamos a velocidade. Sacou?
E para a velocidade escalar, fazemos o módulo da velocidade e depois substituimos na função da posição.
Passo 2
A velocidade é a derivada da posição em relação ao tempo.
Calculando as derivadas
Sendo assim, o vetor velocidade será:
Passo 3
A velocidade para , será
Passo 4
A aceleração é a derivada da velocidade em relação ao tempo.
Calculando a derivada individualmente
O vetor aceleração será:
Passo 5
A aceleração para
Passo 6
A velocidade escalar será o módulo do vetor velocidade, temos .
Para
Passo 7
O gráfico fica da seguinte forma:
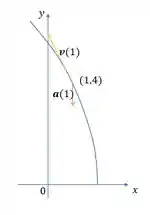
O vetor velocidade indica que a partícula está se movendo para a esquerda (direção negativa no eixo e para cima (direção positiva no eixo ) a partir do ponto .
E o vetor aceleração indica que a partícula está desacelerando na direção (direção negativa no eixo ), enquanto não há mudança na direção (aceleração zero no eixo ).
Resposta
