Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.4 - Ex. 18

(a) Determine o vetor posição de uma partícula dadas a sua aceleração, velocidade e posição iniciais.

(b) Utilize o computador para traçar o caminho percorrido pela partícula.

a → t = t i → + t 2   j → + c o s 2 t k → ,     v → 0 = i → + k → ,     r → 0 = j →

Passo 1

Fala ai galerinha!

Tudo tranquilo? Essa é uma questão bem prática, digo isso porque temos que integrar a posição para encontrar a velocidade, integrar a velocidade para encontrar a aceleração. Viu!?

Na letra B pede-se a curva da partícula, neste caso teremos que pedir ajuda a um software.

Agora é só resolver!

Passo 2

Vamos Integrar a componente do vetor aceleração para termos o vetor velocidade

a t = d v d t

Integrando a ( t ) em relação ao tempo:

v t = ∫ a t d t

v t = ∫ t i + t 2 j + cos ⁡ ( 2 t ) k d t

Passo 3

Integrando termo pôr termo:

- Termo em i

∫ t d t = t ² 2 + C

- Termo em j

∫ t 2 d t = t 3 3 + C

Passo 4

- Termo em k

∫ cos 2 t ⁡ d t

Nesta integral temos que aplicar a integração por substituição.

Considerando u = 2 t . Portanto, a derivada de u em relação a t é:

d u d t = 2

Assim, d t por der expresso como:

d t = d u 2

Podemos substituir na integral

∫ cos u ⁡ d u 2

1 2 ∫ cos u ⁡ d t

A integral será,

= 1 2 s e n   2 t + C

Passo 5

Então a velocidade é:

v t = t 2 2 + C 1 i + t 3 3 + c 2 j + 1 2 s e n   2 t + C 3 k

Usando a condição inicial

v → t = t 2 2 i → + t 3 3   j → + s e n ( 2 t ) 2 k → + C

Em t = 0 , temos que:

v → 0 =   C = i → + k →

Dessa forma, o vetor velocidade procurado é:

v → t = t 2 2 + 1 i → + t 3 3   j → + s e n ( 2 t ) 2 + 1 k → + C

Passo 6

Integrando a componente do vetor velocidade vamos obter o vetor posição

v → t = t 2 2 + 1 i → + t 3 3   j → + s e n ( 2 t ) 2 + 1 k → + C

Integrando termo pôr termo

- Termo em i

∫ t 2 2 + 1 ⁡ d t

= t 3 3 . 1 2 + t

= t 3 6 + t + C 1

- Termo em j

∫ t 3 3 ⁡ d t

= t 4 4 . 1 3

= t 4 12 + C 2

Passo 7

- Termo em k

∫ sen ( 2 t ) 2 + 1 ⁡ d t

∫ s e n ( 2 t ) 2 d t + ∫ d t

1 2 ∫ s e n   ( 2 t )   d t + ∫ d t

Utilizando os mesmos procedimentos do Passo 4 , temos

- c o s ⁡ ( 2 t ) 4 + t + C 3

Passo 8

Então o vetor posição é:

r → t = t 3 6 + t   i → + t 4 12   j → + t - c o s ⁡ ( 2 t ) 4   k → + C

Em t=0, temos que:

r → 0 =   - 1 4 k → + C = j →

Assim, temos que

C = j → + 1 4 k →

Dessa forma, o vetor posição procurado é:

r → t = t 3 6 + t   i → + 1 + t 4 12   j → + 1 4 + t - c o s ⁡ ( 2 t ) 4   k →

Passo 9

Esboçando esse caminho temos a seguinte curva, onde o parâmetro t cresce no sentido anti-horário:

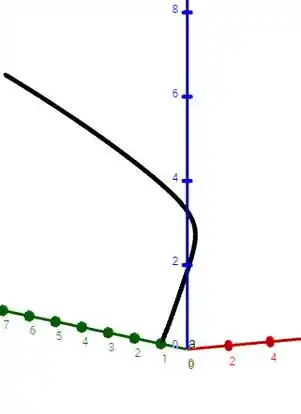
Resposta

Os vetores velocidade e posição procurados são:

v → t = t 2 2 + 1 i → + t 3 3   j → + s e n 2 t 2 + 1 k → + C

r → t = t 3 6 + t   i → + 1 + t 4 12   j → + 1 4 + t - c o s 2 t 4   k →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O módulo do vetor aceleração a é 10c m / s 2 . Use a figura para estimar as componentes tangencial e normal de a .
Duas partículas se movem ao longo das curvas espaciais r 1 t = t , t 2 , t 3 e r 2 t = 1 + 2 t ,1 + 6 t , 1 + 14 t . As partículas colidem? Suas trajetórias se interceptam?
Se dois objetos viajam pelo espaço ao longo de duas curvas diferentes, é sempre importante saber se eles vão colidir. (Um míssil vai atingir seu alvo móvel? Duas aeronaves vão colidir?) As curvas pode
Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de t
Determine os vetores velocidade e aceleração e a velocidade escalar da partícula cuja função posição é dada. r t = 2 i → + e tj → + e - tk →