Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 40
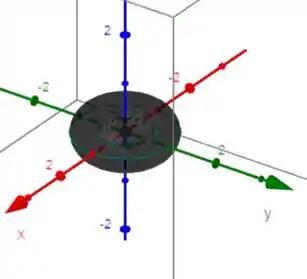
- Determine o volume delimitado pelo toro
- Utilize um computador para desenhar o toro
Passo 1
Olá, pessoal! Tudo bem?
Essa questão tem duas partes. A parte a) pede que a gente encontre o volume contido pelo toro
Caso não saiba, um toro é um volume que se parece com uma rosquinha. Veremos gráficos dele ao decorrer da resolução.
Percebam que a equação do toro foi dada em coordenadas esféricas! Então, a dica é utilizar este sistema de coordenadas para calcularmos o seu volume. Sendo assim, a nossa integral será:
Mas note que não temos os limites de integração dessa integral. Então, usaremos a descrição do toro para definir seus limites em coordenadas cilíndricas e daí podemos resolver nossa integral tripla.
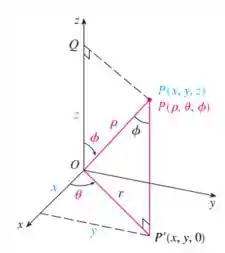
Sistema de coordenadas esféricas
Já a parte da questão pede para que a gente utilize um programa de computador para desenhar nosso toro.
Vamos juntos!
Passo 2
- Nosso trabalho é descrever os limites de integração. E para um toro, ele é dado por:
- : como o próprio enunciado diz:
- : como o toro fica metade na parte positiva do eixo e metade na parte negativa, a variação desse ângulo é:
- : Como a projeção do toro no plano é uma circunferência completa, temos para o ângulo :
Como o toro está centrado na origem, sua variação é:
Portanto, nossa integral é:
Passo 3
Agora, nosso trabalho é calcular a integral definida no final do Passo 2. Sendo assim, temos:
Integrando primeiro em que é a integral de dentro:
Aplicando os limites de integração, temos:
Usando o fato de que:
Substituindo na nossa integral:
Abrindo o termo ao quadrado:
Simplificando em uma soma de frações:
Vamos agora integrar em :
E aplicando os limites de integração:
Finalmente integrando em :
E assim chegamos ao volume de um toro!
Passo 4
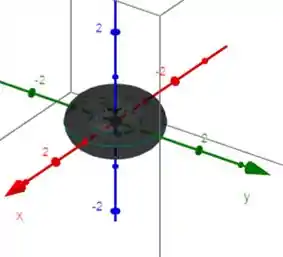
De forma mais simplificada, a imagem abaixo facilita a visualização do toro:
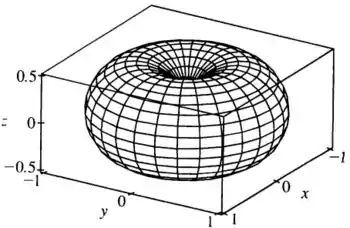
Resposta
