Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.9 - Ex. 19

A figura mostra um campo vetorial F → . Use a interpretação do divergente deduzida nessa seção para determinar se d i v   F → é positivo ou negativo em P 1 e P 2

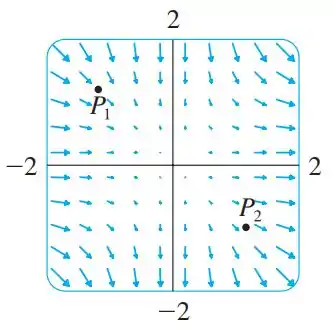
Passo 1

Oi galera, tudo bem? Vamos ver o que a questão quer!

Ela mostra uma figura

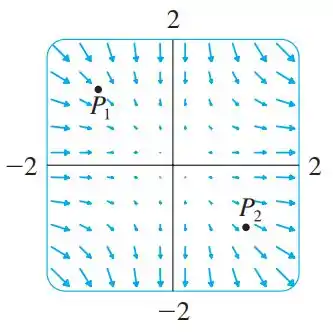
E diz para nós determinarmos se o divergente desse campo vetorial ( d i v   F → ) é positivo ou negativo nos pontos P 1 e P 2 .

Sendo que o divergente pode ser calculado assim:

∇ ⋅ F → = ∂ ∂ x F x + ∂ ∂ y F y

Usando a interpretação do divergente deduzida nessa seção. Certo, mas qual é?

Atenção aqui!!!

O fluxo será positivo quando tivermos a taxa líquida dele saindo.

O fluxo será negativo quando tivermos a taxa líquida dele entrando.

E o divergente acompanha o sinal do fluxo!

Tudo bem, mas o que é a taxa líquida?

É como se fosse o lucro, se entrou mais dinheiro que saiu, você está no lucro! Mas se tratando de fluxo a gente inverte, ou seja, estamos no negativo!

Então, vamos analisar o gráfico vendo essa taxa líquida para cada ponto, ok?

Bora lá?

Passo 2

Vamos analisar esse gráfico.

Primeiro em P 1 :

Observe que as linhas de campo estão que estão chegando nesse ponto são maiores do que as que estão saindo, logo a nossa taxa líquida é do fluxo entrando, ou seja, negativo.

E como vimos, se o fluxo é negativo temos o nosso divergente negativo

∇ ⋅ F → < 0

Passo 3

Agora vamos ao outro ponto.

Dá uma olhada em P 2 :

Observe que as linhas de campo que estão saindo nesse ponto, são maiores que as linhas que estão entrando! Logo a nossa taxa líquida é do fluxo saindo, ou seja, positivo.

E como vimos, se temos um fluxo positivo o nosso divergente é positivo! Portanto

∇ ⋅ F → > 0

Beleza, vamos pra próxima?

Resposta

P 1 :   ∇ ⋅ F → < 0

P 2 :   ∇ ⋅ F → > 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema da Divergência para calcular a integral superfície ∬ SF ⋅ d S , ou seja, calcule o fluxo de F através de S . F x , y , z = x y e z i + x y 2 z 3 j - y e z k S é a superfície da caixa lim
Use o Teorema da Divergência para calcular a integral superfície ∬ S F . d S , ou seja, calcule o fluxo de F através de S . F x , y , z = x 2 y z i + x y 2 z j + x y z 2 k S é a superfície da caixa li
Use o Teorema da Divergência para calcular a integral superfície ∬ SF ⋅ d S , ou seja, calcule o fluxo de F através de S . F = e y tan ⁡ z i + y 3 - x 2 j + x sen ⁡ y k S é a superfície de um sólido q
Use o Teorema da Divergência para calcular a integral superfície ∬ S F . d S , ou seja, calcule o fluxo de F através de S . F = r 2 r ,r = x i + y j + z k S é a esfera com raio R e centrada na origem.
Use o Teorema da Divergência para calcular a integral de superfície ∬ S F ⋅ d S ; ou seja, calcular o fluxo de F através de S . F x , y , z = 3 x y 2 i + x e z j + z 3k , S é a superfície do sólido li