Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 11

Esboce o sólido descrito pelas desigualdades dadas.

2 ≤ ρ ≤ 4 ,   0 ≤ ϕ ≤ π 3 ,   0 ≤ θ ≤ π

Passo 1

Boa tarde galera! Tudo certo? Temos uma três desigualdade

2 ≤ ρ ≤ 4 ,     0 ≤ ϕ ≤ π 3 ,     0 ≤ θ ≤ π

E fomos solicitados a esboçar um sólido, precisamos enxergar uma forma de juntar essas informações e então em um sistema de coordenadas iremos traçar os pontos dessas equações para desenhar o sólido. Vamos lá?

Passo 2

Primeiramente, temos que entender cada coordenadas, veja que 2 ≤ ρ ≤ 4 .

O que isso significa? Significa que o sólido não começa na origem, começa apenas quando o raio for 2 e segue até r = 4

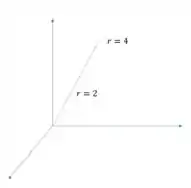
Teremos sólido apenas na região da linha verde. Agora iremos fazer essa linha verde percorrer todo o caminho dos ângulos indicados.

Veja que:

0 ≤ ϕ ≤ π 3 ,

Ou seja, a angulação em relação ao eixo z será de um 60 º . Veja:

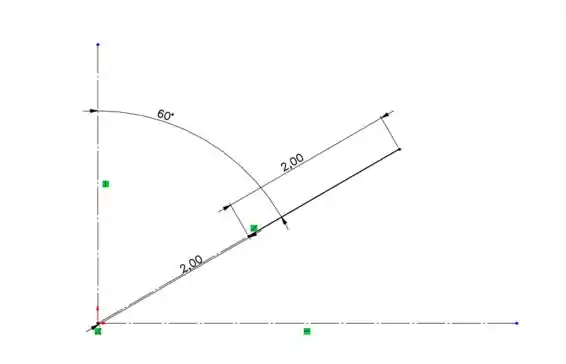
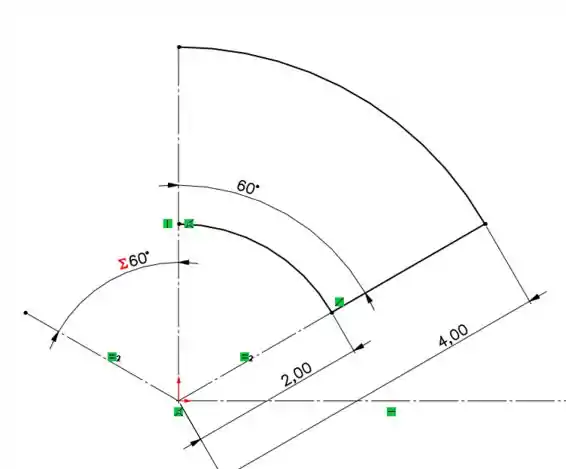
Além disso, temos

0 ≤ θ ≤ π

Então a abertura em relação ao eixo z   será de meia volta completa.

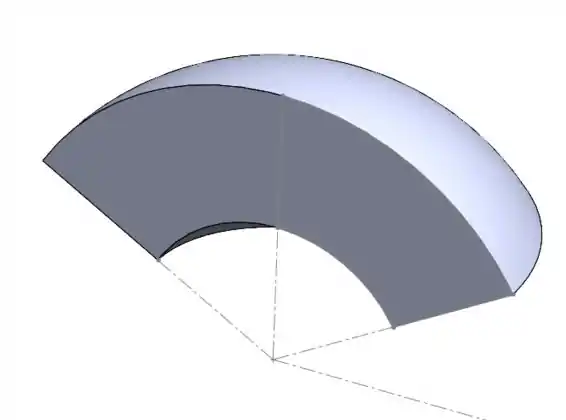
É uma cunha de bolo de forma com um furo no meio, pois não temos ρ indo de zero até algum ponto. Temos que ele sai de 2 e vai até 4, então o “miolo” dele está vazio.

E torno porque o ângulo azimutal vai de zero até π 3 , o que deixa o bolo voando. Saca só no esboço:

Olha e diz se não parece aqueles bolos de laranja? Deu até vontade =)

Olha e diz se não parece aqueles bolos de laranja? Deu até vontade =)

Resposta

Desenho realizado.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use coordenadas esféricas.Determine o volume do sólido que está acima do cone ϕ = π / 3 e embaixo da esfera ρ = 4 cos ⁡ ϕ . E depois encontre o centroide do sólido na parte a).
Use coordenadas esféricas.Calcule o valor de ∭ E x 2 + y 2 + z 2 d V Onde E fica acima do cone z = x 2 + y 2 e entre as esferas x 2 + y 2 + z 2 = 1 e x 2 + y 2 + z 2 = 4 .
Use coordenadas esféricas.Calcule ∭ E x e x 2 + y 2 + z 2 d V , onde E é a porção da bola unitária x 2 + y 2 + z 2 ≤ 1 que fica no primeiro octante.
Encontre a massa e centro de massa de um hemisfério sólido com raio a se a densidade em qualquer ponto for proporcional à sua distância da base.
Use coordenadas esféricas.Encontre o centroide do sólido do Exemplo 4 (assuma densidade constante K ). Encontre o momento de inércia ao redor do eixo z para esse sólido.