Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.2 - Ex. 71

Determine o volume gerado pela rotação de um arco da curva y = s e n x em torno do eixo das abscissas.

Passo 1

Inicialmente, vamos dar uma olhada na função s e n x :

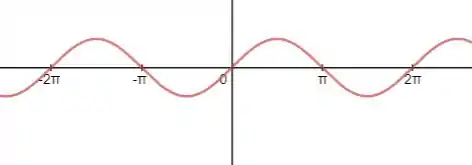
Repare que podemos achar o volume gerador pela curva entre os pontos x = 0 e x = π .

Passo 2

Agora vamos relembrar a expressão para achar o volume:

V = ∫ a b π f x 2 d x

Logo,

V = ∫ 0 π π s e n 2 x d x

Tirando a constante da integral:

V = π ∫ 0 π s e n 2 x d x

Para resolvermos essa integral, temos que lembrar do seguinte:

se n 2 ⁡ x = 1 - cos ⁡ 2 x 2

Assim,

V = π ∫ 0 π 1 - cos ⁡ 2 x 2 d x

Não esquece: ∫ c o s a x   d x = s e n x a + c

Passo 3

Agora vamos partir pra integral!

V = π 2 ∫ 0 π d x - ∫ 0 π cos ⁡ 2 x d x

Integrando:

V = π 2 x - s e n 2 x 2 0 π

Aplicando entre esses pontos:

V = π 2 π - s e n 2 π 2 - 0 - s e n 0 2

Portanto,

V = π 2 2

Resposta

V = π 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral. ∫ cot ⁡ x cos ² ⁡ x d x ²
Avalie a integral. ∫ tan 2 ⁡ x cos 3 ⁡ x d x
Avalie a integral. ∫ sin 5 ⁡ ( 2 t ) cos 2 ⁡ ( 2 t ) d t
Calcule a integral. ∫ s e n 6 x cos 3 ⁡ xd x
Avalie a integral. ∫ t sin ² ⁡ t d t ²