Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 25

Determine o volume do sólido dado.

Abaixo da superfície z = x y e acima do triângulo com vértices ( 1,1 ) , 4,1 e 1,2 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão. Temos que encontrar um volume, ou seja, teremos uma integral dupla de uma função f x , y que será abaixo da superfície. Também precisaremos encontrar uma forma de relacionar os pontos indicados como vértice do triângulo, por ser um triângulo, já começo a pensar em uma equação de uma reta. Vamos começar?

Passo 2

Podemos expressar o volume de um sólido limitado por uma superfície e uma região através da seguinte integral dupla:

V = ∬ D f x , y d A

Onde D é a região limitada na qual devemos integrar a função.

Temos que a equação da superfície é dada por:

z = f x , y = x y

Podemos usar a fórmula da equação de dois pontos para determinar as retas que ligam os vértices e a partir delas encontrar os limites de integração:

y - y 1 = y 2 - y 1 x 2 - x 1 x - x 1

A equação que passa pelos pontos 1,1 e 4,1 é dada por:

y - 1 = 1 - 1 4 - 1 x - 1

y - 1 = 0

y = 1

A equação que passa pelos pontos 1,2 e 4,1 é dada por:

y - 2 = 1 - 2 4 - 1 x - 1

y - 2 = - 1 3 x - 1

3 y - 6 = 1 - x

y = 7 - x 3

Ou seja, sabemos que os limites de integração de y será:

1 ≤ y ≤ 7 - x 3

E para encontrar os limites em relação a x ? Veja a figura que mostra o triângulo.

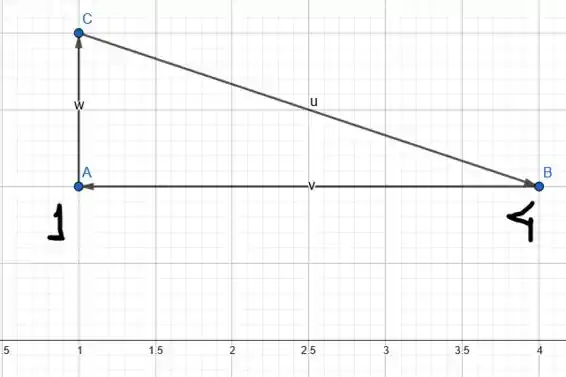
Podemos perceber que os valores de x vão de 1 à 4 . De modo que temos:

1 ≤ x ≤ 4

Passo 3

Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:

D = x , y | 1 ≤ x ≤ 4 ,   1 ≤ y ≤ 7 - x 3

Assim, a integral dupla pode ser escrita como:

V = ∬ D f x , y d A = ∫ 1 4 ∫ 1 7 - x 3 f ( x , y ) d y d x

Como f x , y = z , temos:

V = ∫ 1 4 ∫ 1 7 - x 3 x y d y d x

Vamos resolver a integral de dentro:

∫ 1 7 - x 3 x y d y = x y 2 2 1 7 - x 3

Agora, aplicando os limites de integração, temos:

∫ 1 7 - x 3 x y d y = x 7 - x 3 2 2 - x 1 2 2

∫ 1 7 - x 3 x y d y = x 2 49 + x 2 - 14 x 9 - 1

∫ 1 7 - x 3 x y d y = 1 18 49 x + x 3 - 14 x 2 - 9 x

∫ 1 7 - x 3 x y d y = 40 x + x 3 - 14 x 2 18

Logo, substituindo, temos:

V = ∫ 1 4 ∫ 1 7 - x 3 x y d y d x = ∫ 1 4 40 x + x 3 - 14 x 2 18 d x

Passo 4

Agora é só resolver:

V = ∫ 1 4 40 x + x 3 - 14 x 2 18 d x = 1 18 40 x 2 2 + x 4 4 - 14 x 3 3 1 4

Agora, aplicando os limites de integração, temos:

∫ 1 4 40 x + x 3 - 14 x 2 18 d x = 1 18 40 4 2 2 + 4 4 4 - 14 4 3 3 - 40 1 2 2 + 1 4 4 - 14 1 3 3

Resolvendo, temos:

∫ 1 4 40 x + x 3 - 14 x 2 18 d x = 31 8  

Portanto, o volume será:

V = 31 8

Resposta

V = 31 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície.A parte do paraboloide hiperbólico z = y 2 - x 2 que está entre os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 4 .
Determine a área da superfície.A parte do plano 2 x + 5 y + z = 10 que está dentro do cilindro x 2 + y 2 = 9 .
Determine a área da superfície.A parte do plano 3 x + 2 y + z = 6 que está no primeiro octante.
Mostre que a área da parte do plano z = a x + b y + c que projeta sobre uma região D no plano x y com área A ( D ) é a 2 + b 2 + 1 A ( D ) .
Determine a área da superfície.A parte da superfície z = 1 + 3 x + 2 y 2 que está acima do triângulo com vértices 0,0 , 0,1 e 2,1 .