Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 35

Determine o volume do sólido por subtração de dois volumes.

O sólido limitado pelos cilindros parabólicos y = 1 - x 2 , y = x 2 - 1 e pelos planos x + y + z = 2 , 2 x + 2 y - z + 10 = 0 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão, temos que fazer uma subtração do volume de dois sólidos, para isso vamos ter que uma integral dupla. O processo para resolver essa integral dupla exige o conhecimento dos limites de integração, então essa será a primeira etapa, após isso iremos identificar as funções necessárias para integrar e então faremos a operação de subtração.

Passo 2

O primeiro passo é esboçar as curvas para identificar os pontos de intersecção:

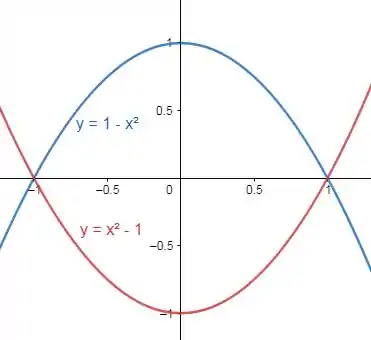
Veja que as funções se interceptam em x =   - 1 e x = 1 , sendo que a função y = x 2 - 1 é sempre a função inferior nessa região de interesse. Ou seja, podemos definir que os limites de integração serão:

- 1 ≤ x ≤ 1

E

x 2 - 1   ≤ y ≤ 1 - x 2

Passo 3

Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:

D = x , y | - 1 ≤ x ≤ 1   , x 2 - 1 ≤ y ≤ 1 - x 2  

Assim, a integral dupla pode ser escrita como:

V = ∬ D f x , y d A = ∫ - 1 1 ∫ x 2 - 1 1 - x 2 f ( x , y ) d y d x

Sabendo que V = V 2 - V 1 precisamos saber quem será V 2 e quem será V 1 .

Vamos escrever as funções dos planos:

- x - y + 2 = z  

2 x + 2 y + 10 = z

Substituindo para x = - 1 e y = 1 - 1 = 0

1 + 2 = 3

- 2 + 10 = 8

Para x = 0 ,   y = - 1

Temos o seguinte:

1 + 2 = 3

- 2 + 10 = 8

Ou seja, é possível notar que:

2 - x - y < 2 x + 2 y + 10

Portanto:

V 2 = ∫ - 1 1 ∫ x 2 - 1 1 - x 2 2 x + 2 y + 10 d y d x

E:

V 1 = ∫ - 1 1 ∫ x 2 - 1 1 - x 2 2 - x - y d y d x

Logo:

V = ∫ - 1 1 ∫ x 2 - 1 1 - x 2 2 x + 2 y + 10 - 2 - x - y d y d x

V = ∫ - 1 1 ∫ x 2 - 1 1 - x 2 3 x + 3 y + 8 d y d x

Vamos resolver a integral de dentro:

∫ x 2 - 1 1 - x 2 3 x + 3 y + 8 d y = 3 x y + 3 y 2 2 + 8 y x 2 - 1 1 - x 2

Agora, aplicando os limites de integração, temos:

∫ x 2 - 1 1 - x 2 3 x + 3 y + 8 d y = 3 x 1 - x 2 + 3 1 - x 2 2 2 + 8 1 - x 2 - 3 x x 2 - 1 + 3 x 2 - 1 2 2 + 8 x 2 - 1

∫ x 2 - 1 1 - x 2 3 x + 3 y + 8 d y = 6 x - 6 x 3 + 16 - 16 x 2

Logo, substituindo, temos:

∫ - 1 1 ∫ x 2 - 1 1 - x 2 3 x + 3 y + 8 d y d x = ∫ - 1 1 6 x - 6 x 3 + 16 - 16 x 2 d x

Passo 4

Agora é só resolver:

V = ∫ - 1 1 6 x - 6 x 3 + 16 - 16 x 2 d x = 3 x 2 - 3 2 x ~ 4 + 16 z - 16 3 x 3 - 1 1

Fazendo as contas, temos:

V = 64 3

Resposta

V = 64 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido no primeiro octante limitado pelo cilindro z = 16 - x 2 e pelo plano y = 5 .
Determine o volume do sólido limitado pelo paraboloide z = 2 + x 2 + y - 2 2 e pelos planos z = 1 , x = ± 1 , y = 0ey = 4 .
Determine o volume do sólido que está abaixo da superfície z = 1 + x 2 y e y e os planos z = 0 , x = ± 1 , y = 0ey = 1 .
Determine o volume do sólido que se encontra abaixo do plano 4 x + 6 y - 2 z + 15 = 0 e acima do retângulo R = { x , y ,- 1 ≤ x ≤ 2e - 1 ≤ y ≤ 1 } .
Determine o volume do sólido que se encontra abaixo do paraboloide hiperbólico z = 3 y 2 - x 2 + 2 , e acima do retângulo R = - 1,1 × [ 1 , 2 ] .