Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.6 - Ex. 7
Determine a área da superfície.
A parte do paraboloide hiperbólico que está entre os cilindros e .
Passo 1
E aiii turminha, tudo bem com vocês? Vamos nessa!!!
Temos que determinar a área da superfície que compreende parte do paraboloide hiperbólico:
,
e está entre os dois cilindros abaixo:
Vish, aprece difícil essa. Como eu começo?
Vamos com calma pensar juntos, beleza?
Você lembra que podemos calcular a área de uma superfície através da seguinte integral:
Onde, .
Repare que temos dentro da raiz uma função que precisa ser deriva em relação a e . Como o enunciado nos uma função de que compreende a região, basta fazermos as derivadas, beleza?
Agora precisamos pensar na região de integração. Ela nos diz que está entre dois cilindros, certo? Logo podemos pensar em utilizar coordenadas cilíndricas:
Isso vai facilitar muito nossa integração.
Sabendo disso, precisamos determinar os intervalos de integração do raio e do ângulo. Observe que é um cilindro completo, não tem nenhuma restrição.
Assim, sabemos que o ângulo varia de até . Já para o raio, observe que temos um cilindro menor de raio igual a e um cilindro maior de raio igual a . Logo, temos que:
Agora podemos resolver tranquilo essa ein!!! Vamos lá!
Passo 2
Sabemos que nossa função é:
Vamos determinar primeiramente as derivadas parciais da função . Sendo assim
Portanto, devemos resolver a seguinte integral:
Simplificando, temos que:
Passo 3
Nossa região está entre os dois cilindros:
Observe o esboço feito no Geogebra:
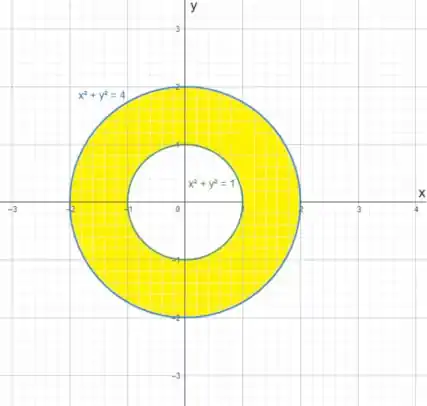
Nossa região de interesse é a região em amarelo, que está entre os dois círculos. Quero que você perceba que o intervalo de raio está entre a superfície interna até a superfície externa.
Como estamos trabalhando em uma região cilíndrica, é conveniente descrevê-la em coordenadas cilíndricas.
Portanto, temos os seguintes limites:
Passo 4
Agora vamos escrever a integral em coordenadas cilíndricas.
Substituindo as variáveis, vamos ter:
Agora precisamos resolver a integral, e lembra que sempre começamos integrando de dentro para fora.
Integrando em . Aqui vamos com calma, pois precisamos fazer uma substituição do tipo:
Substituindo na integral, temos:
Integrando em , e voltando a variável . Vamos ter:
Aplicando os limites de integração, ficamos com:
Repare que ficamos com uma integral simples em . Integrando vamos ter:
Aplicando os limites de integração, vamos ter:
Simplificando, nossa resposta é: