Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 34
Encontre o volume aproximado do sólido no primeiro octante limitado pelos planos , e e pelo cilindro . (Utilize uma ferramenta gráfica para estimar os pontos de interesecção.)
Passo 1
Oi pessoal, tudo bem? Vamos recordar o que é primeiro octante?
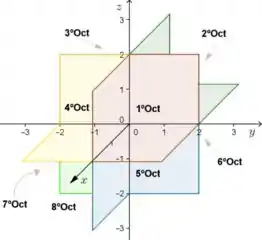De maneira semelhante ao primeiro quadrante, o primeiro octante, também é a região no gráfico em que todas as coordenadas são positivas, porém, para gráficos de 3 coordenadas. (Ou seja, em “3D”). Portanto é necessário que fique claro que iremos considerar apenas os valores positivos de cada eixo.
Vamos agora analisar essa questão, temos um sólido qualquer limitado pelos planos indicados no enunciado e queremos encontrar o volume. Para encontrar o volume de um sólido nós fazemos a seguinte integral dupla:
Mas para isso, precisamos definir quem é a função e quais são esses limites de integração. Agora que já está claro o processo que será tomado, vamos por a mão na massa?!
Passo 2
O primeiro passo é esboçar as curvas para identificar os pontos de intersecção:
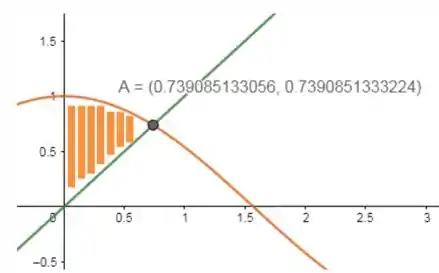
Nossa área de interesse é a área hachurada de laranja. Veja que as funções se interceptam em , além disso, veja que a função em verde é a função inferior para toda a região de interesse, enquanto a função é a função superior. O que nos mostra que:
Enquanto que
Passo 3
Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:
Assim, a integral dupla pode ser escrita como:
Como , temos:
Vamos resolver a integral de dentro:
Agora, aplicando os limites de integração, temos:
Logo, substituindo, temos:
Passo 4
Agora é só resolver:
Assim, lembrando que a primitiva de é , temos que: