Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.3 - Ex. 19
Determine o volume do sólido dado.
19.
Abaixo do paraboloide e acima da região delimitada por e
Passo 1
Fala, gente. Tudo show?
A questão quer o volume do sólido através de informações sobre um paraboloide e regiões delimitadas por e
A região D que iremos calcular é a intersecção que aparece no gráfico abaixo
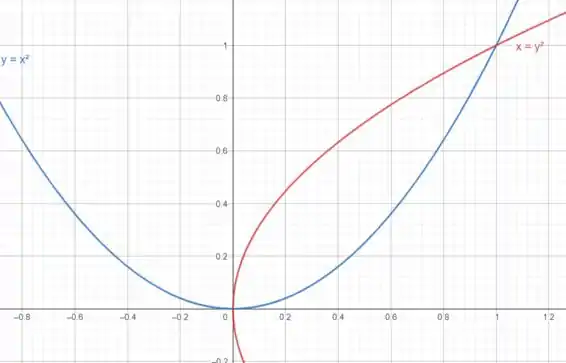
Podemos escrevê-la como uma região do Tipo I ou Tipo II.
Lembra que, no Tipo I, é como se nossa região fizesse uma “sombra” no eixo . Já no tipo II, a “sombra” é no eixo .
Vamos escolher ela como do Tipo I, show?
Isolando uma das variáveis em uma das equações dadas, vamos utilizar e isolar na equação
Substituindo na outra equação
Como só assume valores positivos
Elevando os dois lados ao quadrado temos
Temos então que
E
Substituindo em para encontrar os pontos
Então os pontos de intersecção são e e podemos escrever a como
Ou seja, com isso encontramos os limites de integração.
Passo 2
Temos que o volume do sólido , restrito abaixo de na região , é dado por
Observe que, como estamos numa região Tipo I, faremos uma integral .
Agora vamos calcular a integral de dentro, primeiro em relação a
Substituindo os limites de integração:
Agora integrando em relação a
Pela divisão de frações, invertemos o denominador e multiplicamos.
Fazendo o M.M.C. por termos denominadores diferentes na soma de frações,