Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 14.6 - Ex. 58
Mostre que as pirâmides cortadas do primeiro octante por qualquer plano tangente à superfície em pontos do primeiro octante têm todas o mesmo volume.
Passo 1
Oie, meu amigo. Vamos juntos resolver essa atividade hoje.
Queremos provar aqui, que os volumes para todas as pirâmides no primeiro octante, cortada pelo plano tangente a superfície:
Tem o mesmo volume.
Podemos determinar a equação do plano tangente a uma superfície de nível do tipo em pela fórmula desta seção
No nosso caso temos que
e . Vamos então encontrar a equação dessa superfície tangente, depois iremos encontrar os pontos de interceptação com os eixos no primeiro octante.
Passo 2
Calculando as derivadas parciais:
Veja que a derivada parcial é dada derivando em relação a variável que queremos, e considerando todas as outras como constantes:
Substituindo na equação do plano:
Substituindo:
Distribuindo as multiplicações:
Teremos:
Passo 3
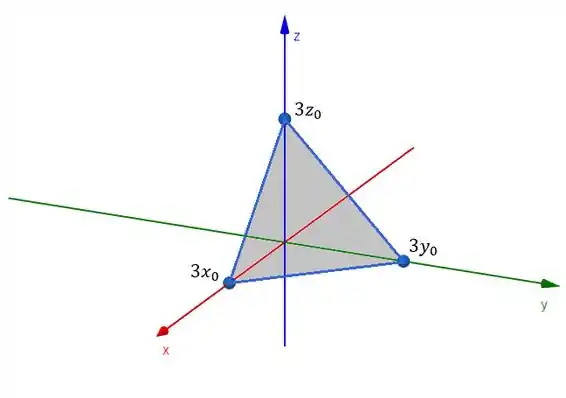
Agora vamos achar os vértices da pirâmide. Um deles é a origem, já que a pirâmide é limitada pelo primeiro octante. Para achar os outros, vamos zerar duas variáveis e encontrar quanto vale a terceira:
Para e :
Para e :
Para e :
Então temos a seguinte pirâmide
Passo 4
O volume da pirâmide é dado por:
Onde é a área da base
E temos que , então o volume da pirâmide é:
Mas como obedece , temos que , logo
Ou seja, o volume da pirâmide não depende do ponto que gera o plano tangente.