Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 23
Determine o volume do sólido dado.
Abaixo do plano e acima da região limitada pelas parábolas e .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão, temos que encontrar um volume, o que já indica a possibilidade de integral dupla, temos a equação de um plano que teremos que transforma em nossa função , temos também os limites de integração dado em função de e , então nosso procedimento envolve relacionar as funções das parábolas para encontrar os valores em que essas parábolas estão de fato limitada.
Vamos começar?
Passo 2
Podemos expressar o volume de um sólido limitado por um plano e uma região através da seguinte integral dupla:
Onde é a região limitada na qual devemos integrar a função.
Podemos reescrever a equação do plano da seguinte maneira:
Esta equação será o nosso .
Para encontrar os limites de integração vamos relacionar as parábolas dadas:
Ora, se:
eEntão:
Encontramos os limites em . De modo que é
E qual os limites para ?
Veja a imagem:
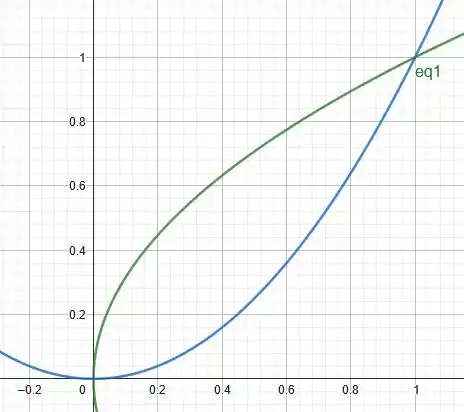
A função inferior em azul é a função . A função superior em verde é a função que é o mesmo que . Ou seja, os limites em são:
Passo 3
Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:
Assim, a integral dupla pode ser escrita como:
Como , temos:
Vamos resolver a integral de dentro:
Agora, aplicando os limites de integração, temos:
Logo, substituindo, temos:
Passo 4
Agora é só resolver:
Agora, aplicando os limites de integração, temos:
Resolvendo, temos:
Portanto, o volume será: