Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 20
Determine o volume do sólido dado.
20.
Abaixo da superfície e acima da região limitada por e .
Passo 1
Fala, galera. Tudo show?
O enunciado pede pra determinar o volume de um sólido que está abaixo de uma superfície e acima de região limitada por e . Moleza, né?
Primeiro passo é desenharmos essa região.
Temos e , portanto:
Colocando em evidência
Assim descobrimos que no eixo a região será definida em
Substituindo esses pontos, teremos no eixo as delimitações dessa região também
Pegando qualquer uma das equações,
Assim,
Tendo esses pontos que delimitam a região que estamos calculando e nossas equações dos planos, chegamos a esse gráfico:
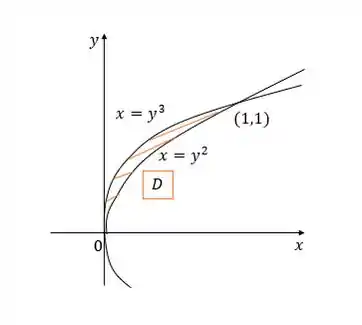
Veja que estamos trabalhando num plano , e isso quer dizer pra gente que .
Passo 2
Lembra que questão quer o volume de um sólido? Temos uma fórmula para isso, assim ó:
E quem é nosso ? Basicamente nosso , já que também pode ser representado assim:
Veja que estamos trabalhando num plano , e isso quer dizer pra gente que .
Logo,
Então essa é a função que estará dentro da nossa integral dupla? Com certeza!
O único problema agora é achar os limites de integração.
Vamos considerar a nossa região como de Tipo II.
Explicando melhor, é como se nossa região fizesse uma “sombra” no eixo , e ali temos exatamente nossos limites de integração bem definidos.
Já que não temos limites de integração definidos para o eixo , observamos pelo gráfico acima que as duas equações se encontram até o ponto na abscissa.
Assim, podemos escrever a integral da seguinte forma:
Agora, basta calcular.
Passo 3
Como temos uma integral dupla, começamos resolvendo de fora para dentro, olha só:
Primeiro em relação a :
Substituindo os limites de integração:
Agora integrando em relação a