Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 27
Determine o volume do sólido dado.
27.
Limitada pelos planos coordenados e pelo plano
Passo 1
Fala, galera!
A questão pede pra gente determinar o volume de um sólido, limitado pelos planos coordenados e por esse outro plano aqui, ó:
Mas que sólido é esse?? Calma lá.
Sabemos que o volume é definido porque trabalhamos com três eixos (, correto?
Vamos considerar os planos coordenados como
Como nas integrais duplas, calculamos a integral de uma função , precisamos achar a intersecção do plano dado com o plano , para analizarmos a região de integração.
Passo 2
Para descobrir nossos planos cartesianos, vamos fazer algumas substituições dessa função acima.
Quando
Isolando
Com isso, quando
E quando
Então a reta se intersecta no eixo nos pontos e e podemos escrever a região da seguinte forma
Ou representando num gráfico, ficará assim:
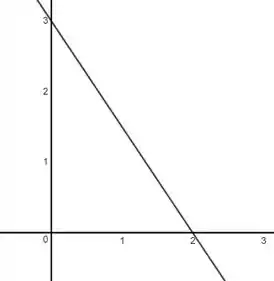
Essa é a região que estamos calculando.
Passo 3
Para saber a função que iremos integrar, basta isolar na equação do plano
Temos então que o volume do sólido , que é restrito abaixo de na região , é dado por
Passo 4
Agora vamos integrar, primeiro em :
Agora iremos integrar em relação a :