Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 28
Determine o volume do sólido dado.
Limitada pelos planos , , e
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!
Para resolver este problema, primeiro vamos identificar cada uma das retas e planos. O plano é onde nossa região de integração estará. Então, precisamos encontrar a região usando as outras duas equações.
Vamos começar com a equação . Isolando , será obtido . Em seguida, encontramos o ponto de intersecção com . E substituindo na equação conseguiremos encontrar o valor de e .
Passo 2
Neste caso, a função que vamos integrar, vai sair da equação
O plano é onde a nossa região de integração vai estar, então para achar a região , vamos usar as outras duas equações.
Usando , vamos isolar uma das variáveis
Para achar o ponto de intersecção com , vamos substituir na equação:
Substituindo para achar o :
Passo 3
Olhando no plano, temos:
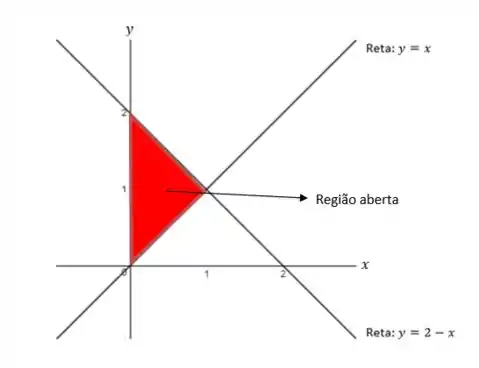
Ainda temos uma região aberta, para isso, vamos ter que achar a intersecção de com o plano , que basta substituir e temos .
Temos então, como região, o triangulo de vértices. , e e podemos escrever como uma região do tipo I da seguinte forma
Passo 4
Temos então que o volume do solido que é restrito abaixo de na região é dado por
Agora vamos integrar, primeiro em :
Em seguida, integramos em relação a :