Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 29
Determine o volume do sólido dado.
Limitada pelos cilindros , e pelos planos ,
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!
Neste caso, a função que vamos integrar é a equação porque estamos lidando com um sólido delimitado pelos cilindros e , além dos planos e .
A equação descreve a forma tridimensional do sólido ao longo do eixo , onde a altura do sólido em relação ao plano é determinada pelo quadrado da coordenada . Essa relação é a base para calcularmos o volume do sólido através de integração.
Passo 2
Vamos analisar as equações e no plano .
Substituindo na equação :
Assim, encontramos:
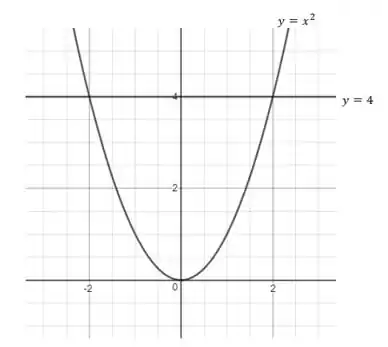
Dessa forma, a região no plano pode ser descrita como uma região do tipo I da seguinte forma:
Passo 3
Agora, vamos configurar a integral dupla para calcular o volume do solido que é restrito abaixo de na região :
Agora vamos integrar, primeiro em relação a :
Portanto, a integral se torna:
Passo 4
Agora em relação a
Vamos resolver cada um separadamente.
Para a primeira integral:
Então sem a constante:
Então:
Passo 5
Para a segunda integral:
Assim, temos:
Para subtrair essas frações, encontramos um denominador comum:
Portanto: