Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 30
Determine o volume do sólido dado.
Limitado pelo cilindro e os planos , , no primeiro octante.
Passo 1
Vamos lá galera, temos que resolver o volume de um sólido. Para isso precisamos entender como expressar a função desse sólido matematicamente e como escrever os limites de integração dupla a partir dos planos informados. Mas primeiro de tudo para resolvermos essa questão será necessário entendermos o que é primeiro octante.
Vamos nos lembrar do conceito de quadrante. Tente pensar no sistema de coordenadas para dois eixos, o eixo X o Y. Temos que o primeiro quadrante é a região no gráfico em que as coordenadas X e Y são positivas.
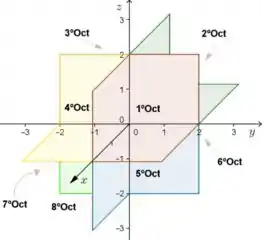
De maneira semelhante, o primeiro octante, também é a região no gráfico em que todas as coordenadas são positivas, porém, para gráficos de 3 coordenadas. (Ou seja, em “3D”). Portanto é necessário que fique claro que iremos considerar apenas os valores positivos de cada eixo.
Passo 2
Podemos expressar o volume de um sólido limitado por uma superfície e uma região através da seguinte integral dupla:
Onde é a região limitada na qual devemos integrar a função.
Neste caso, a função que vamos integrar, vai sair da equação:
Isolando , temos:
Como estamos falando do primeiro octante, , então:
Para descobrir os limites de , temos que, como :
Como , então:
E os limites de integração em ? Ora se os planos são , , , então é certo que é limitado inferiormente em e superiormente em . De modo que:
Passo 3
Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:
Assim, a integral dupla pode ser escrita como:
Como , temos:
Vamos resolver a integral de dentro:
Agora, aplicando os limites de integração, temos:
Logo, substituindo, temos:
Passo 4
Agora é só resolver por substituição:
Vamos chamar . Logo:
Analisando os limites, temos que, quando:
A substituição será:
Agora, aplicando os limites de integração, temos:
Resolvendo, temos:
Logo:
Portanto, o volume será: