Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.5 - Ex. 22

Resolva a equação diferencial e use uma calculadora gráfica ou um computador para traçar vários membros da família de soluções. Como a curva solução muda quando C varia?

x y ' = x 2 + 2 y

Passo 1

Temos que a equação diferencial linear   x y ' = x 2 + 2 y , pode ser escrita da seguinte forma:

y ' + P x y = Q ( x )

y ' + 2 x y = x

Para resolvelá podemos utilizar o fator integrante

I x = e ∫ P x d x = e ∫ 2 x d x = e - 2 l n ⁡ | x | = ( e ln ⁡ x ) - 2 = 1 x 2

Multiplicando ambos os lados da equação diferencial linear por I ( x ) :

1 x 2 y ' + 2 x ³ y = 1 x

O primeiro termo se parece muito com uma derivada pela regra do produto então podemos escreve-lo da seguinte forma:

d d x 1 x ² y = 1 x

Integrando ambos os lados obtemos:

1 x 2 y = ∫ 1 x d x = ln ⁡ x + C

y = x 2 ln ⁡ x + x ² C

Passo 2

Construindo o gráfico para C = 0 ,   C = 1 2 e C = - 1 2 :

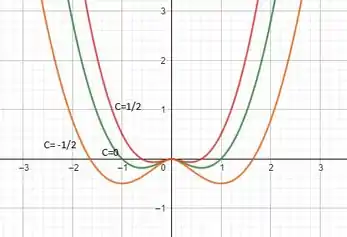
Quando C é maior que zero a curva fica menor e mais fechada tendendo a uma parábola, já quando C é menor que zero a curva fica maior e mais aberta.

Resposta

y = x 2 ln ⁡ x + x ² C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva a equação diferencial.4 x^3 y + x^4 y^' = sen^3 x
Resolva o problema de valor inicial.x^2 y ' + 2 x y = ln x , y (1) = 2
O sistema de equações diferenciais d x d t = 0,5 x - 0,0004 x 2 - 0,001 x y d y d t = 0,4 y - 0,001 y 2 - 0,002 x y É um modelo para as populações de duas espécies.(a) O modelo descreve cooperação, ou
Moscas, sapos e crocodilos coexistem em um ambiente. Para sobreviver, os sapos precisam comer as moscas e os crocodilos precisam comer os sapos. Na ausência de sapos, a população de moscas crescerá ex
Determine se a equação diferencial é linear.y^' = (1)/(x) + (1)/(y)