Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 12
Encontre a área da superfície.
A parte da esfera que está dentro do paraboloide .
Passo 1
Fala, gente boa! Tudo show?
Nessa questão, precisamos encontrar a área de superfície definida pela esfera
Que tem parte dentro do paraboloide
A figura a seguir esquematiza a região de interseção entre a esfera e o paraboloide.
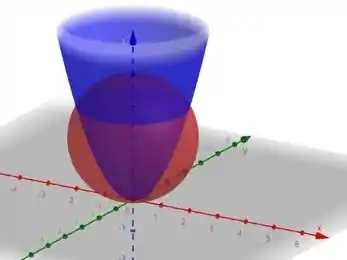
Pra gente encontrar essa área, usaremos essa fórmula aqui:
Iremos encontrar os limites de integração dessa região , as derivadas e e jogar na fórmula. Show!
Passo 2
Descobrindo os limites de integração, vamos começar substituindo a equação do paraboloide na equação da esfera. Temos:
Logo, esses são os dois planos que interceptam a esfera (conforme podemos verificar na imagem acima), no entanto, podemos reescrever a equação da esfera como:
Completando o quadrado em adicionando dos dois lados, temos:
Sendo assim, substituindo a equação para o plano , temos:
Dessa forma, podemos notar que o raio da região de interseção será um círculo ao redor da origem com raio variando de a .
Passo 3
Com isso, temos também que:
Com isso, faremos as derivadas parciais, em relação a e em relação a :
Sendo assim, a área da superfície pode ser escrita como:
Conforme visto no passo 1, a região fornecida no enunciado é delimitada por um círculo, sendo assim, podemos mudar o sistema de coordenadas cartesianas para polar, com
Fazendo isso, temos:
Organizando...
Fazendo o M.M.C. dentro da raiz...
Colocando para cima a raiz, ficaremos com expoente negativo:
Passo 4
Resolvendo a integral obtida no passo anterior, de dentro para fora, temos:
Substituindo os limites de integração:
Simplificando a expressão, obtemos:
Show de bola! 😉