Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 11

Encontre a área da superfície.

A parte da esfera x 2 + y 2 + z 2 = a 2 que se encontra dentro do cilindro x 2 + y 2 = a x e acima do plano x y .

Passo 1

Fala aí! Nesse exercício iremos analisar a parte da esfera x 2 + y 2 + z 2 = a 2 que fica abaixo do cilindro x 2 + y 2 = a x e acima do plano x y .

Para facilitar a visualização, vamos dar uma olhada na figura a seguir que esquematiza a região de interseção entre a esfera e o cilindro:

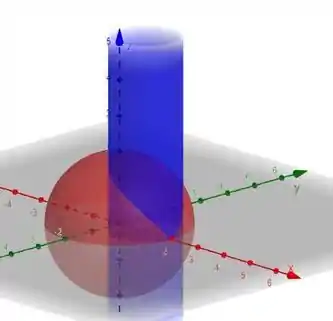
Pela equação nós podemos ver que o raio da região de interseção vai ficar em função de a e de θ , pois estamos em uma esfera, né?

Além disso, a região vai ficar somente no lado positivo do eixo x , então θ irá variar de - π / 2 até π / 2 , show?

Passo 2

Agora vamos para as continhas! Vamos fazer o seguinte:

z 2 = a 2 - x 2 - y 2

z = a 2 - x 2 - y 2 = f x , y

Fazendo as derivadas parciais teremos:

f x = d d x a 2 - x 2 - y 2   f y = d d y a 2 - x 2 - y 2

f x = - x a 2 - x 2 - y 2 - 1 / 2     f y = - y a 2 - x 2 - y 2 - 1 / 2

Sendo assim, podemos achar a área da superfície assim:

A S = ∬ - x a 2 - x 2 - y 2 - 1 2 2 + - y a 2 - x 2 - y 2 - 1 2 2 + 1   d A

Conforme visto no passo 1, a região fornecida no enunciado é delimitada por um círculo, sendo assim, podemos mudar o sistema de coordenadas cartesianas para polar, só pra facilitar as continhas, tá bom?

Pra fazer essa conversão, vamos lembrar que:

x = r   c o s   θ y = r   s e n   θ

Com as novas coordenadas, vamos ter que:

f x = - r   c o s   θ a 2 - r   c o s   θ 2 - r   s e n   θ 2 - 1 / 2  

  f y = - r   s e n   θ a 2 - r   c o s   θ 2 - r   s e n   θ 2 - 1 / 2

Então teremos que:

∫ - π / 2 π / 2 ∫ 0 a c o s θ r 2   .   c o s ²   θ   a 2 - r 2 + r 2   .   s e n ²   θ   a 2 - r 2 + 1   r d r d θ

∫ - π / 2 π / 2 ∫ 0 a c o s θ r 2 a 2 - r 2 + 1   r d r d θ

∫ - π / 2 π / 2 ∫ 0 a c o s θ r 2 + a 2 - r 2 a 2 - r 2   r d r d θ

∫ - π / 2 π / 2 ∫ 0 a c o s θ a a 2 - r 2   r d r d θ

∫ - π / 2 π / 2 ∫ 0 a c o s θ a r a 2 - r 2 - 1 / 2 d r d θ

Passo 3

Resolvendo a integral temos:

∫ - π 2 π 2 - a a 2 - r 2 1 2 r = 0 r = a c o s θ d θ

  ∫ - π 2 π 2 - a a 2 - a 2 c o s ² θ   - 1 2 - a d θ

Colocando o a em evidência dentro da raiz e simplificando a expressão, obtemos:

  ∫ - π 2 π 2 - a a 2 1 - c o s ² θ   - 1 2 - a d θ

  ∫ - π 2 π 2 a ² 1 - 1 - c o s ² θ   - 1 2 d θ

a 2 ∫ - π / 2 π / 2 1 - 1 - c o s ² θ   d θ

Lembrando das propriedades da integral, sabemos que:

∫ - a a d x = 2 ∫ 0 a d x

Com isso e através da relação fundamental onde s e n ² x   + c o s ² x   = 1 podemos reescrever a integral de cima como:

2 a 2 ∫ 0 π / 2 1 - 1 - c o s ² θ   d θ

2 a 2 ∫ 0 π / 2 1 - s e n   θ d θ

2 a 2 θ + c o s   θ   0 π / 2

2 a 2 π 2 + 0 - 0 + 1

a 2 ( π - 2 )

Sendo assim, a área da superfície é:

A S = a 2 ( π - 2 )

Show de bola! Conseguimos!

Resposta

A S = a 2 ( π - 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 2 - x 2 - y 2 d y d x
Desenhe o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 4 - x - 2 y d x d y
Use um sistema algébrico computacional para encontrar o valor exato da integral ∬ R x 5 y 3 e x y d A , onde R = 0,1 × 0,1 . Então use um CAS para desenhar o sólido que é dado pela integral.
Encontre o volume do sólido limitado pela superfície z = x 2 + x y 2 e os planos z = 0 , x = ± 1 , y = 0 e y = ± 2 .
Represente graficamente o sólido que se encontra entre a superfície z = 2 x y / ( x 2 + 1 ) e o plano z = x + 2 y e é limitada pelos planos x = 0 , x = 2 , y = 0 e y = 4 . Então encontre o volume.