Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 37

Determine o volume do sólido por subtração de dois volumes.

O sólido sob o plano z = 3 , acima do plano z = y e entre os cilindros carabólicos y = x 2 e y = 1 - x 2 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão, temos que definir qual a integral dupla resolve o volume para um sólido limitado sob o plano z = 3 e subtrair o volume do sólido inferior z = y . Mas para isso, precisaremos identificar quais os limites de integração.Vamos colocar a mão na massa?

Passo 2

Vamos resolver as equações parabólicas:

x 2 = 1 - x 2

x 2 = 1 2

x = ± 1 2

x = ± 1 2

Vamos ver como é a aparência dessas funções?

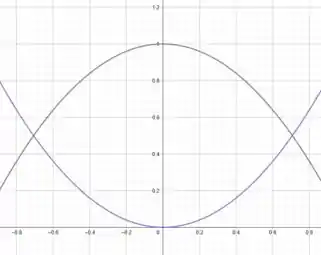
Perceba que a função y = x 2 sempre será a função inferior na área de interesse, de modo que é o nosso limite inferior de integração. E a função y = 1 - x 2 será a função superior.

Passo 3

Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:

D = x , y | - 1 2 ≤ x ≤ 1 2   , x 2 ≤ y ≤ 1 - x 2  

Assim, a integral dupla pode ser escrita como:

V = ∬ D f x , y d A = ∫ - 1 / 2 1 / 2 ∫ x 2 1 - x 2 f ( x , y ) d y d x

Temos que o volume do nosso sólido será uma subtração entre os volumes dos sólidos limitados pelos planos z = 3 e z = y . Teremos então:

∫ - 1 / 2 1 / 2 ∫ x 2 1 - x 2 3 d y d x -   ∫ - 1 / 2 1 / 2 ∫ x 2 1 - x 2 y d y d x

Pelo teorema fundamental do cálculo, sabemos que:

∫ a + b   d x =   ∫ a   d x + ∫ b   d x

Podemos fazer então:

V = ∫ - 1 / 2 1 / 2 ∫ x 2 1 - x 2 3 - y d y d x

Vamos resolver a integral de dentro:

∫ x 2 1 - x 2 3 - y d y = 3 y - y 2 2 x 2 1 - x 2

Agora, aplicando os limites de integração, temos:

∫ x 2 1 - x 2 3 - y d y = 3 1 - x 2 - 1 - x 2 2 2 - 3 x 2 - x 2 2 2

∫ x 2 1 - x 2 3 - y d y = 5 2 - 5 x 2

Logo, substituindo, temos:

∫ - 1 / 2 1 / 2 ∫ x 2 1 - x 2 3 - y d y d x = ∫ - 1 / 2 1 / 2 5 2 - 5 x 2 d x

Passo 4

Agora é só resolver:

V = ∫ - 1 / 2 1 / 2 5 2 - 5 x 2 d x = 5 2 x - 5 x 3 3 - 1 / 2 1 / 2

Fazendo as contas, temos:

V = 5 2 3

Resposta

V = 5 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3 . Utilizando o teorema de Pappus (veja Vol. 1, 5.ª edição), calcule o volumedo sólido obtido pela rotação, em torno da reta dada, do conjunto B dado.a. B é o círculo x 2+y 2≤1ey=x+2 a reta.
3 . Utilizando o teorema de Pappus (veja Vol. 1, 5.ª edição), calcule o volumedo sólido obtido pela rotação, em torno da reta dada, do conjunto B dado.b. B é o conjunto de todos (x, y) tais que x 2≤y≤
Calcule o volume do sólido, no primeiro octante, limitado pelas superfícies z = 1 - y 2 , x = y 2 + 1 e x = - y 2 + 9 .
Determine a área da região limitada pelas curvas: ax = y 3 , x + y = 2 e y = 0 .
Calcule o volume do sólido limitado pelas superfícies y = 4 - x 2 , y = 3 x , z = x + 4 e z = 0 .