Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 36
Determine o volume do sólido por subtração de dois volumes.
O sólido limitado pelo paraboloide cilíndrico e pelos planos ,.
Passo 1
Oii, galerinha! Tudo tranquilo?
A questão pede pra gente achar o volume do sólido limitado pelo paraboloide cilíndrico
e pelos planos
,
Para achar o volume de um sólido abaixo de uma função aplicamos a integral:
Para esse tipo de questão, vale analisarmos o volume dos sólidos e o diagrama da região plana no plano acima do qual o sólido se encontra. Esse plano é onde está a região , e como nossa integral dupla é em , é do gráfico do plano que vamos tirar os limites de integração para finalmente resolver a questão.
Depois, podemos resolver a integral dupla em relação a e a , usando a ordem que tornar a integral mais fácil. Daí é só resolvermos a integral dupla como uma integral iterada. Uma integral iterada é uma integral calculada sequencialmente, uma após a outra. Para resolver integrais duplas a gente começa “de dentro pra fora”.
Vamos em frente!
Passo 2
Vamos começar entendendo nossos limites de integração. O gráfico tridimensional dos planos e sólidos dados no enunciado:
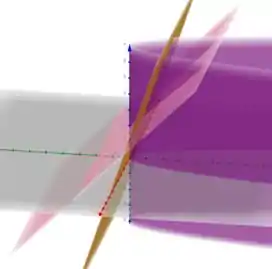
Aqui nosso parabolóide cilíndrico está em roxo e temos os dois planos , , respectivamente, alaranjado e rosa.
Agora vamos entender como essas curvas se comportam no plano , de onde sairá nossa região e seus limites de integração. Para funções que já dependem de e , como:
Podemos plotar diretamente essa curva. Os planos, como dependem de e , precisamos de uma análise para entender como eles se projetam no plano.
Vamos então igualar os planos para entendermos onde eles se interceptam. Lembra que nosso sólido está limitado pelos dois planos? Então a análise do plano vai até onde os planos se cruzam. Esse é o limite da região .
,
Igualando os planos:
Resolvendo a equação, teremos:
Assim, nossa região é:
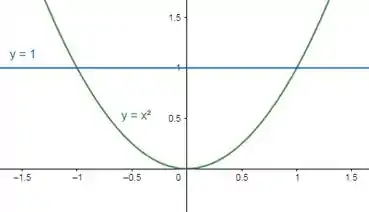
Passo 3
Pelo gráfico, podemos ver que as curvas se interceptam em e .
Assim, a integral dupla pode ser escrita como:
E aqui nós deixamos a integral em função de “por dentro”, já que temos termos que dependem de nos limites de integração de .
Sabendo que precisamos saber quem será e quem será . Fazendo uma simples observação, é possível notar que:
Vimos ali na imagem que um plano está mais atrás do outro, então vamos chamar o sólido limitado pelo plano maior de e o sólido limitado pelo plano menor . Olhando o gráfico tridimensional, notamos que:
Portanto:
E:
Como o sólido que estamos procurando está confinado entre os dois planos, subtraímos um volume do outro, para obter o volume que queremos:
Vamos resolver a integral de dentro:
Agora, aplicando os limites de integração, temos:
Logo, substituindo, temos:
Passo 4
Agora é só resolver:
Fazendo as contas, temos: