Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 7

Calcule o volume do sólido limitado pelas superfícies y = 4 - x 2 , y = 3 x , z = x + 4 e z = 0 .

Passo 1

E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D

Sabemos que a integral dupla representa geometricamente o volume de uma região no espaço. Chamando essa região de D , matematicamente, o seu volume será dado por:

V = ∫ ∫ D f x ,   y d x d y

O que precisamos saber para fazer o cálculo é a função z = f x ,   y e se a região é do tipo 1 (contínua em x e com y limitada entre funções de x ) ou do tipo 2 (contínua em y e com x limitada entre funções de y ).

Assim, com as curvas dadas no enunciado, podemos determinar os limites de integração e a função z que representa a região.

Passo 2

Como o exercício já nos dá a função z , sabemos que:

f x ,   y = z = x + 4

Cujo esboço está a seguir:

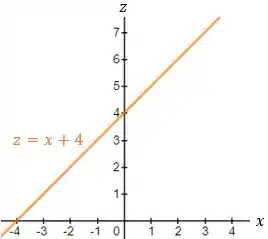
Para z ≥ 0 :

x ≥ - 4

E igualando as equações de y , temos:

4 - x 2 = 3 x → x 2 + 3 x - 4 = 0

Essa função de segundo grau nos dá as raízes:

x = - 3 ± 9 + 16 2 = - 3 ± 25 2

Ou seja:

x 1 = - 3 + 5 2 = 1

E:

x 2 = - 3 - 5 2 = - 4

Portanto, o intervalo de integração de x é:

- 4 ≤ x ≤ 1

Passo 3

Além disso, nós temos y definida como funções de x , o que mostra que a região é do tipo 1 . Para sabermos qual equação de y é o limite superior e qual é o limite inferior da integração, vamos esboçar ambas essas equações e fazer essa análise.

Logo, o esboço é:

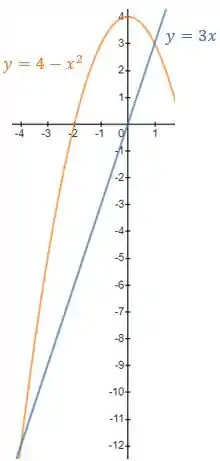
Tal que, para - 4 ≤ x ≤ 1 , y será dado como:

3 x ≤ y ≤ 4 - x 2

Com isso, o volume do sólido pode ser dado por:

V = ∫ - 4 1 ∫ 3 x 4 - x 2 x + 4 d y d x = ∫ - 4 1 x + 4 ∫ 3 x 4 - x 2 d y d x

Passo 4

Então, resolvendo a integral interna:

V = ∫ - 4 1 x + 4 ∫ 3 x 4 - x 2 d y d x = ∫ - 4 1 x + 4 y | 4 - x 2 3 x d x

E substituindo os intervalos de integração, temos:

V = ∫ - 4 1 x + 4 4 - x 2 - 3 x d x

⇒ V = ∫ - 4 1 x + 4 - x 2 - 3 x + 4 d x

Ou seja:

V = ∫ - 4 1 - x 3 - 7 x 2 - 8 x + 16 d x

Passo 5

Assim, a última integral resultará em:

V = ∫ - 4 1 - x 3 - 7 x 2 - 8 x + 16 d x = - x 4 4 - 7 x 3 3 - 4 x 2 + 16 x | 1 - 4

Substituindo os limites de integração:

V = - 1 4 - 7 3 - 4 + 16 - - 64 + 448 3 - 64 - 64

⇒ V = - 1 4 - 7 3 - 448 3 + 192 + 12 = - 1 4 - 7 3 - 448 3 + 204

Portanto, encontrando o MMC:

V = - 3 - 28 - 1792 + 2448 1 2 = 625 12

Resposta

V = 625 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume aproximado do sólido no primeiro octante limitado pelos planos y = x , z = 0 e z = x e pelo cilindro y = cos ⁡ x . (Utilize uma ferramenta gráfica para estimar os pontos de interesec
Determine o volume do sólido dado.Abaixo da superfície z = 1 + x 2 y 2 e acima da região limitada por x = y 2 e x = 4
Determine o volume do sólido dado.Abaixo da superfície z = x y e acima do triângulo com vértices ( 1,1 ) , 4,1 e 1,2 .
Determine o volume do sólido dado.Abaixo do plano 3 x + 2 y - z = 0 e acima da região limitada pelas parábolas y = x 2 e x = y 2 .
Determine o volume do sólido dado.Limitada pelo paraboloide z = x 2 + y 2 + 1 e os planos x = 0 , y = 0 , z = 0 e x + y = 2 .