Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 5b
Determine a área da região limitada pelas curvas:
, e .
Passo 1
E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D
Sabemos que a integral dupla representa geometricamente o volume de uma região no espaço. Então, como a área possui uma dimensão a menos que o volume, ela pode ser representada por uma única integral simples:
Assim, com as curvas dadas no enunciado, podemos determinar os limites de integração e a função de que representa a região.
Passo 2
Dessa forma, a primeira coisa a se fazer é o esboço da nossa região que é dada por:
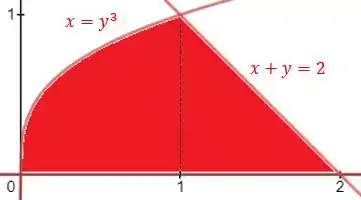
Podemos perceber que ela possui uma mudança de forma em (uma curva à esquerda e um triângulo retângulo à direita). Então, iremos separá-la em duas regiões diferentes, sendo que a área de cada uma será representa por integrais diferentes.
O próximo passo é definir a função de cada curva. Então, dizendo que a região à esquerda é a região , a sua curva é dada por:
Já a curva da região (região à direita) é dada por:
Mas como ela possui a forma exata de um triângulo retângulo e nós sabemos as dimensões em cada variável, podemos aplicar a fórmula da área de um triângulo de forma direta. Então a sua área será dada por:
Passo 3
Com isso, vamos calcular a integral da primeira região que pode ser escrita como:
Aqui, o seu intervalo de integração está bem definido no esboço da região, tal que:
Então, resolvendo a integral:
E substituindo os intervalos de integração, temos:
Passo 4
Já para a segunda região, o cálculo é bem mais fácil:
Passo 5
Por fim, sabemos que a nossa região é dada pela interseção dessas duas regiões que consideramos. Então, a área total é a soma das áreas de cada região, ou seja:
Portanto:
Encontrando o MMC: