Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.3 - Ex. 3-a
3 . Utilizando o teorema de Pappus (veja Vol. 1, 5.ª edição), calcule o volumedo sólido obtido pela rotação, em torno da reta dada, do conjunto B dado.
a. B é o círculo a reta.
Passo 1
O teorema de Pappus diz que
Onde é a distância entre o centro do nosso objeto a reta
A Area do objeto que estamos rotacionando
Passo 2
Neste item vamos calcular
Na reta
De cara podemos Calcular a área da nossa superfície.
Passo 3
Geometricamente teremos
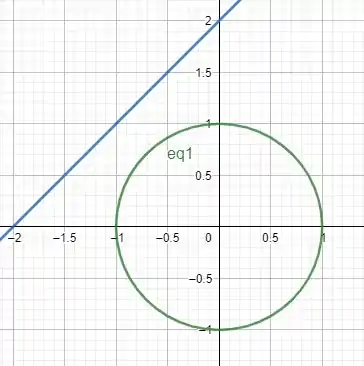
Queremos no caso a distancia do Ponto (0,0) ate a reta. E como já vimos em geometria analítica, a menor distancia é a que é perpendicular a reta e transpassa o ponto, ou seja a reta cinza
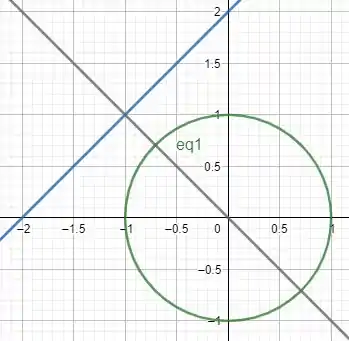
Logo podemos concluir que
Assim
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Exercícios de Livros Relacionados
Use um sistema de computação algébrico para determinar o volume exato do sólido.Abaixo da superfície z = x 3 y 4 + x y 2 e acima da região limitada pelas curvas y = x 3 - x e y = x 2 + x para x ≥ 0 .
Calcule ∫ ∫ D 1 - x 2 - y 2d A , onde D é o disco x 2 + y 2 ≤ 1 , identificando primeiro a integral como o volume de um sólido.
Desenhe o sólido limitado pelo plano x + y + z = 1 e pelo paraboloide z = 4 - x 2 - y 2 e determine seu volume exato. (Utilize seu SCA para fazer esse desenho, para achar as equações das fronteiras da
Utilize coordenadas polares para determinar o volume do sólido dado.Dentro da esfera x 2 + y 2 + z 2 = 16 e fora do cilindro x 2 + y 2 = 4 .
19. Utilize coordenadas polares para determinar o volume do sólido. Abaixo do cone z = x 2 + y 2 e acima do disco x 2 + y 2 ≤ 4 .