Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.3 - Ex. 3-b
3 . Utilizando o teorema de Pappus (veja Vol. 1, 5.ª edição), calcule o volumedo sólido obtido pela rotação, em torno da reta dada, do conjunto B dado.
b. B é o conjunto de todos (x, y) tais que e y = x - 1 a reta.
Passo 1
O teorema de Pappus diz que
Onde é a distância entre o centro do nosso objeto a reta
A Area do objeto que estamos rotacionando
Passo 2
Neste item vamos calcular
Na reta
Para calcular área e o centro de massa dessa superfície não sera tao trivial. Afinal nossa superfície é
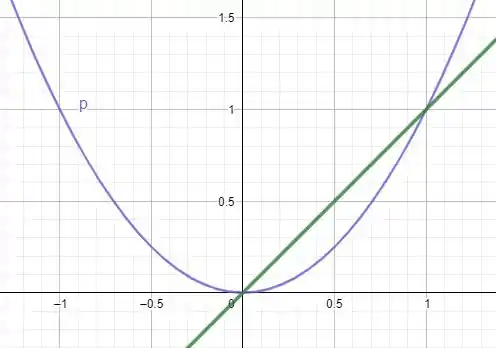
A interseção dessas duas curvas no intervalo
Assim a área sera
Passo 3
Geometricamente teremos
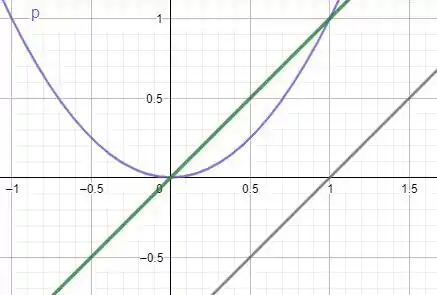
Precisamos primeiro descobrir o centro de massa e depois descobrir distancia de ponto a reta. O centro de massa pode ser calculado como
Onde é a densidade da nossa superfície, que podemos definir como
Como o enunciado não nos diz nada a respeito dessa Massa, podemos assumir como homogênea e igual a 1, obtendo por fim
Passo 4
Vamos calcular o centro de massa, começando por x
Agora vamos calcular o centro de y
Passo 5
Agora so nos resta calcular distancia entre ponto a reta, nosso ponto é
E nossa reta
Nossa equação da distancia é
Por fim podemos calcular o nosso volume
Terminamos por aqui. Te vejo na próxima resolução
: )