Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 21
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo
Passo 1
A curva que ele deu é:
Elevando ao quadrado para retirar a raiz:
Assim, essa curva é a circunferência de raio centrada na origem, mas vamos pegar apenas a parte acima do eixo porque a função é a raiz positiva.
Para entendermos como é a região e qual vai ser a integral, vamos olhar um esboço dela:
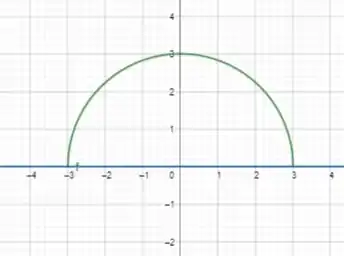
A região é entre a curva verde e a azul.
Entao a região vai de até . Onde o raio do disco vai ser a função verde:
O volume vai ser:
Como a expressão da circunferência é a parte positiva, vamos ter:
Passo 2
Vamos resolver essa integral:
Primeiro, vamos ver a integral indefinida:
Passo 3
Voltando para a nossa integral definida:
Resposta
Exercícios de Livros Relacionados
(Teorema de Papus para a elipse.) Considere que o conjunto A de todos os pontos (x,y) tais que ( x - α ) 2 a 2 + y - β 2 b 2 ≤ 1a ≥ 0eb ≥ 0 e situado no semiplano y ≥ 0 . Mostre que o volume do sólido
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 1 2 ≤ x ≤ 2 e 0 ≤ y ≤ 1 x 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 1 x ≤ y ≤ 1e1 ≤ x ≤ 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : 0 ≤ y ≤ xex 2 + y 2 ≤ 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : y ≥ 0 ,1 ≤ x ≤ 2ex 2 - y 2 ≥ 1